284 (18)

568 22. Zastosowanie przekształcenia Fouriera

Funkcja /(t) może przybierać wartości zespolone, wobec tego |/(t)|² = /(£)/*({), gdzie f* oznacza liczbę zespoloną sprzężoną z f Biorąc pod uwagę wzór (22.3), mamy

J l/(OI²dt = J /(0/*(0d£ = — J /*(£)[ 1 F(a>)e**da>]dt =

— on    — m    — rr\    - rn

+ 00 + 00 | +00 +00

“ do    —oo

Na podstawie wzoru F(co) = j f(t)e ^j“‘df wnioskujemy, że

+ 00

(22.24) wobec tego

+ 00

J |/(t)|²d£ = ^- J F(co)F*(co)dcu,

- rrt    — no

skąd wynika wzór (22.23), bowiem F(co)F*(a>) = |F(co)|².

+ Q0

T UU

Wzór Parsevala ma bardzo ciekawą interpretację fizyczną. Całkę J |/(f)|²df

— oo

można traktować jako energię przekształconą na ciepło w oporniku o rezystancji R = 1£2 przy przepływie prądu i =/(t) w nieskończenie wielkim przedziale czaso-

J 1- 00

wym( — co, + oo). Zgodnie ze wzorem (22.23) wyrażenie— f |F(c«)|² dco przedstawia

_ oo

Tównież tę energię. Przyjmujemy, że w części widma pulsacji między co a co+dci)

1    1 ⁺⁰°

zawarta jest energia — |F(co)|²dco. Wyrażenie — f |F(co)|²dco przedstawia zatem ²ⁿ    2n

energię zawartą w całym widmie pulsacji od — oo do + oo. W związku z tym można mówić o rozkładzie energii w widmie pulsacji od — oo do + oo, a wielkość — |F(co)|²

jest nazywana gęstością widmową energii. Należy zwrócić uwagę, że często gęstością widmową energii nazywa się wielkość |F(co)|² bez współczynnika l/2n, która przedstawia gęstość widmową energii w widmie częstotliwości / = co/2rt.

Twierdzenie 11 (o transformacie funkcji impulsowej Diraca). Jeżeli f(t) jest funkcją ciągłą zmiennej rzeczywistej t, to spełniony jest wzór

2 71

(22.25)

J /(f)<5(£-r)dr=/(T),

~ 00

gdzie 5(r) oznacza funkcję impulsową Diraca (por. p. 16.7.1).

Zależność (22.25) wyraża własność filtrującą (odsiewającą) funkcji impulsowej Diraca, polegającą na wybraniu jednej wartości /(t) funkcji/(t) odpowiadającej wartości t = t z nieskończonego przedziału zmiennej niezależnej.

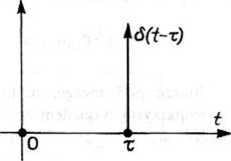
Rys. 22.1. Wykres przesuniętej funkcji impulsowej Diraca

Wyznaczymy transformatę Fouriera funkcji Diraca <5(t —t) przedstawionej na rys. 22.1. Zgodnie z określeniem przekształcenia Fouriera mamy

t)} = f <5(t-T)e-^j0"dr,

— oo

a po uwzględnieniu wzoru (22.25), otrzymujemy

P{5(t-T)} = e-^jfl".    (22.26)

W szczególnym przypadku, jeżeli r = O, to

F{S(t)} = 1.    (22.27)

Stwierdzamy zatem, że transformata Fouriera funkcji impulsowej Diraca <5(t) jest taka sama, jak transformata przekształcenia Laplace a.

22.3. Przykłady obliczania gęstości widmowej

Przykład 1. Wyznaczymy gęstość widmową sygnału o postaci funkcji Gaussa

f(t) = Acxp

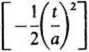
(22.28)

przy założeniu, że A oraz a są liczbami dodatnimi. Przebieg sygnału o postaci funkcji Gaussa przedstawiony jest na rys. 22.2

J

Rys. 22.2 Przebieg sygnału o postaci funkcji Gaussa