288 (16)

576 22. Zastosowanie przekształcenia Fouriera

biegunów. W dalszych rozważaniach ograniczymy się tylko do funkcji meromorficz-

nych.

Na płaszczyźnie zmiennej zespolonej rozpatrzymy krzywe zamknięte C_t oraz C₂ utworzone przez odcinek osi urojonej i przez półokrąg o promieniu R położony po prawej (rys. 22.14a) lub lewej (rys. 22.14b) stronie osi urojonej na płaszczyźnie

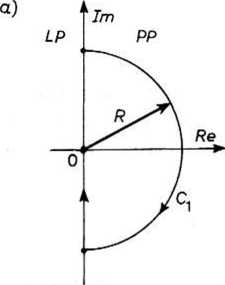
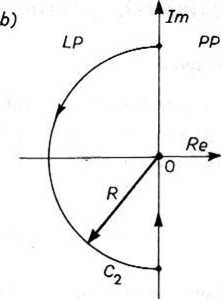
Rys. 22.14. Krzywe zamknięte na płaszczyźnie zmiennej zespolonej (opis w tekście)

zmiennej zespolonej. Gdy F -»oo, wówczas krzywe zamknięte C₁ oraz C₂ obejmują odpowiednio prawą półpłaszczyznę PP lub lewą półpłaszczyznę LP zmiennej zespolonej s.

Można udowodnić, że jeżeli funkcja s^vF(s/j)-+k < co, gdy s-»oc dla v > 1, to lim 2~j )e^s'ds, gdy t < 0,'

(22.37)

f(t) = 1

Ci

lim ——: (pff* )e*'ds, gdy t > 0. 2tcj J

Ci

Zgodnie z twierdzeniem Cauchy’ego o residuach, całka wzdłuż zorientowanej dodatnio krzywej zamkniętej równa się sumie residuów w biegunach zawartych w obszarze ograniczonym tą krzywą. W granicy, gdy R-+ oo, wówczas krzywe C_l oraz C₂ obejmują odpowiednio półpłaszczyznę PP lub LP, wobec tego przy obliczaniu całek wzdłuż tych krzywych wchodzą w grę sumy residuów w biegunach zawartych w całej półpłaszczyźnie PP lub LP. Otrzymuje się zatem

FI 7 )e^sl

-I res

w bieg. PP

gdy    t < 0,

gdy    t > 0.

Znak minus w zależności dla t < 0 wynika stąd, że krzywa C, w półpłaszczyźnie PP

J(t) = A

Z ^res

w bieg. LP

F( j )e^s'

(22.38)

z przyjętym zwrotem, wnętrze jej znajduje się po prawej stronie. Oznacza to, że funkcja /(r) dla t < 0 jest równa pomnożonej przez — 1 sumie residuów funkcji f (v j)e^s' we wszystkich biegunach znajdujących się w półpłaszczyźnie PP po prawej stronie osi urojonej. Natomiast funkcja/(f) dla t > 0 równa się sumie residuów we wszystkich biegunach znajdujących się w półpłaszczyźnie LP po lewej stronie osi urojonej.

Residuum funkcji F(s/j)e^s' w biegunie wielokrotnym s = s_k o krotności n oblicza się ze wzoru

res

S = Sk

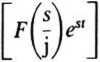
_1_f d"’¹

(n— ljljds'’^-1

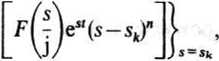
(22.39)

a w biegunie jednokrotnym (n = 1)

(22.40)

Przykład. Obliczymy oryginał funkcji

f(s) =

1

(s —2)²(s + 3)

Funkcja F(s) ma dwa bieguny, a mianowicie biegun dwukrotny s = 2 w prawej półpłaszczyźnie PP oraz biegun jednokrotny s = —3 w lewej półpłaszczyźnie LP. Zgodnie ze wzorami (22.39) i (22.40), residua w tych biegunach wynoszą:

res [F(s)e“] = — IjT--₂--(s-2)²]}    =—["—1    =—(5t-l)e²',

.=2    1 • \ds|_(s— 2)²(s + 3)'    Jj_s=2 dsLs+3j„₂ 25

res [F(s)e“] = ——    Ó+3)

,= -j    (s-2)²(s+3)

1

~25°

Na podstawie wzoru (22.38) otrzymujemy zatem

-(1 — 5t)e^2ty    gdy t < 0,

f(t) =

25

1

—e 25

gdy t > 0.

Po obliczeniu granicy lewo- i prawostronnej tej funkcji w punkcie f = 0, znajdujemy

fi0 ) = /(O^-) = 125.

22.4.3. Wzór całkowy

Do wzoru (22.34) podstawiamy F(a>) = Fj(a>)— }F₂(a>) z zależności (22.6) oraz = coswf4-jsinurt, otrzymując

1 ^+x

/(^f) ⁼ 2^ 1 [F,(tu)cos<yr-FF2(cu)sin(ur]da)-F

| +00

+.ir~ f fF. fa»)sina»r — F, (o;) cos ruf Ideo.