290 (16)

580 22. Zastosowanie przekształcenia Fouriera

Przekształcenie Fouriera ma pewne zalety w porównaniu z transformacją Laplace’a. Mianowicie przekształcenie Fouriera dotyczy funkcji f(t) określonych w przedziale ( — 00, + 00), podczas gdy przekształcenie Laplace’a dotyczy funkcji określonych w przedziale (0, 00). Kolejną zaletą przekształcenia Fouriera jest możliwość stosowania w obliczeniach transmitancji widmowej, którą można wyznaczyć na drodze eksperymentalnej. Odpowiedź y(r) układu na wymuszenie x(t) można wówczas wyznaczyć na podstawie wzoru

y(t) = -*- f T{j(o)X((o)^^atd(o    (22.48)

^-00

wynikającego z zależności (22.47) i (22.3), a całkę zawartą w tym wzorze można obliczyć w sposób przybliżony na drodze numerycznej.

Natomiast wadą przekształcenia Fouriera jest warunek bezwzględnej całkowal-ności funkcji/(f) w przedziale nieskończonym ( — oo, + 00). Wskutek tego przekształcenie Fouriera istnieje dla dość wąskiej klasy funkcji.

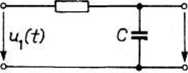
Przykład. Wyznaczymy odpowiedź u₂(t) układu z rys. 22.17 na wymuszenie u,(£) = U_ce~^fiUI, gdzie /? > 0, którego przebieg podaje rys. 22.18.

R

U₂(i)

Rys. 22.17. Przykład obwodu elektrycznego

Gęstość widmowa wymuszenia

+ co    0    1 OC

X{m) = J U₀e *e“^j,a'dt = U₀ J e^{tf j}“>'dt + U₀ J^- e^_</!+J"^,'dt = U₀

- co    — oo    0

wobec tego

---1-

1

p-j(i) P+jcoj

2U₀P P²+a>¹

Łatwo sprawdzić, żc transmitancja układu z rys. 22.17 wyraża się wzorem

T(s) =

1 «

1+sCR x+s gdzie a — 1 /CR, a więc transmitancja widmowa

T(]w) =

a

a +j(')

Zgodnie ze wzorem (22.47), gęstość widmowa odpowjedzi rozpatrywanego układu wynosi

l'M =

2 U₀xfi

(a+jw)()V²+(0²)'

W celu obliczenia przekształcenia odwrotnego, za pomocą residuów, podstawiamy jco = s, czyli oj = —js do powyższego wyrażenia, otrzymując

2 U₀*p

2 U₀*P

j/    <s + x)(0²-s²) (s + a)(s+/S) (s-/?)'

Funkcja ta ma jeden biegun jednokrotny s, = /i w prawej półpłaszczyźnie i dwa bieguny jednokrotne Sj = —a oraz s₃ = —/? w lewej półpłaszczyźnie zmiennej zespolonej, gdy a # /i. Łatwo sprawdzić, że założenia konieczne przy obliczaniu przekształcenia odwrotnego są spełnione. Residua w poszczególnych biegunach wynoszą:

“I#"]-"

2v₀*pe(s-p)

(s + Z){s + P)(s~P) 2L/₀a/łe”(s + a)

s = p

(s + z)(s + p)(s~P) 2 U₀*pt*l3 + p)

(s + a) {s + P)(s — P)

Zgodnie z wzorem (22.38) otrzymujemy

u

z+P ’

2l/₀a/?e~” ~(z-p)(z + p)’

t/oW*

s=-0

z+P '		gdy	t <0
*-p\	Z + p )	gdy	t > 0

yU) =

Na podstawie tych zależności sprawdzamy, że

a + 0

y(0-) = y(0⁺)

22.6. Gęstość widmowa funkcji okresowych

22.6.1. Zależności podstawowe

Przekształcenie Fouriera funkcji okresowych nie istnieje w zwykłym sensie, ze względu na rozbieżność całki

T|/W|dt.

— 00

Jednakże możliwe jest przekształcenie funkcji okresowych za pomocą transformacji Fouriera w ujęciu teorii dystrybucji.