26 (316)

I? Sztuka argumentacji - Krzysztof Szymanek, Krzysztof A. Wieczorek, Andrzej S. Wójcik - iLibrary Reader				. fii x)
on 'u?	a	ęP P3 k ^Limit wydruku: 0	Strona 26/150	S O 0 ^

K. S*)min;k. K. A. WKcecrik. A. S. HWjcifc Jfeiuhi di^atematfL ÓtitaiM* u A*AwA» ar%umcmóh. Wjrwuo . 20KI. ISBN S? 01 • 14069 U. C by WN PWN 200}

26 Podstawowe zagadnienia_

Diagram powyższego argumentu przedstawia się następująco:

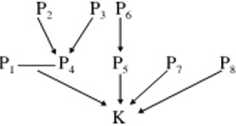
W powyższym przykładzie mamy do czynienia z dwoma podargumentami. W pierwszym z nich zdania P, i P, stanowią przesłanki dla konkluzji pośredniej P₄. w drugim przesłanka P₆ uzasadnia konkluzje pośrednią P_s. Argument główny składa się z konkluzji K oraz przesłanek P,, P₄, P_v P₇, P_g. Przesłanki P, oraz P₄ wspierają konkluzję w sposób łączny, zaś P<, P₇ oraz P_K niezależnie.

Zadanie 3.3.3.

Zbudować diagramy argumentów z przykładu 3.1.1.

Zadanie 3.3.4.

a)    Zbudować diagramy wszystkich argumentów złożonych z zadań i przykładów rozdziałów 2 oraz 3.

b)    Zbudować diagram argumentu:

Kto chce przejść odległość siu metrów, musi najpierw przejść połowę lej odległości, co zajmie pewien czas Tpotem połowę pozostałego dystansu, co zajmie czas 7\; potem połowę pozostałego dystansu, co zajmie czas T, — i tak dalej. Przejście odległości stu metrów wiąże się więc z kolejnym przebywaniem nieskończenie wielu odcinków drogi, konkretnie odcinków kolejno 50 m, 25 m. 12,5 m, 6,25 m, 3,125 m, itd. Przebycie każdej następnej „połowy połowy ” drogi Zjujmuje pewien czas, który co prawda jest coraz krótszy, ale zawsze większy (fd 0. Łączny czas przebycia całości drogi wyraża się więc liczbą będącą sumą nieskończenie wielu większych od zera liczb: T, + T_: + T_f + T₄ +... Ponieważ suma nieskończenie wielu większych od zera liczb jest nieskończenie wielka, w ięc czas przebycia całości dystansu jest nieskończony. i\ie jest więc możliwe przebycie odległości 100 metrów.

Start

<- Gra FreeCell #30416

$ 25-Paint

j? Itelix iLibrary Reader

EP Sztuka argumentacji .

12:47