290 291 (8)

290

Czftt III. Podstawy makroekonomii

Rozdział 10. Wzrost {mpoilarrn

291

Z* *

ZATRUONIENIE

Rysunek 10.3 jest ilustracją graficzną równania (10.19). Na rysunku szkicuje, my dwie funkcje: liniową g(m) = óm oraz funkcję inwestycji w przeliczeniu na jednego zatrudnionego h (m) = s₀f(m). Rozwiązanie równania (10.19) odpowiada współrzędnym punktu przecięcia prostej i krzywej. Z rysunku 10.3 wynika również, iż jeśli inwestycje na jednego zatrudnionego byłyby wyższe od ubytku technicznego uzbrojenia pracy, to wówczas poziom technicznego uzbrojenia pracy byłby niższy od m*. W rezultacie procesów dostosowawczych, techniczne uzbrojenie pracy będzie rosło, aż do osiągnięcia poziomu m*.

Czynnikiem dostosowującym proporcje makrogospodarczc (reprezentowane przez skłonność do oszczędzania i stopę zużycia kapitału) do techniki produkcji (reprezentowanej przez funkcję wydajności pracy) jest techniczne uzbrojenie pracy. Oznacza to. że dla określonej wartości skłonności do oszczędzania s₀ i stopy zużycia kapitału d istnieje taki poziom technicznego uzbrojenia pracy nt^m, przy którym gospodarka znajduje się w stanie równowagi stacjonarnej. Oczywiście, zmiany skłonności do oszczędzania albo stopy zużycia kapitału muszą powodować zmiany technicznego uzbrojenia pracy, o ile ma być zachowana równowaga stacjonarna.

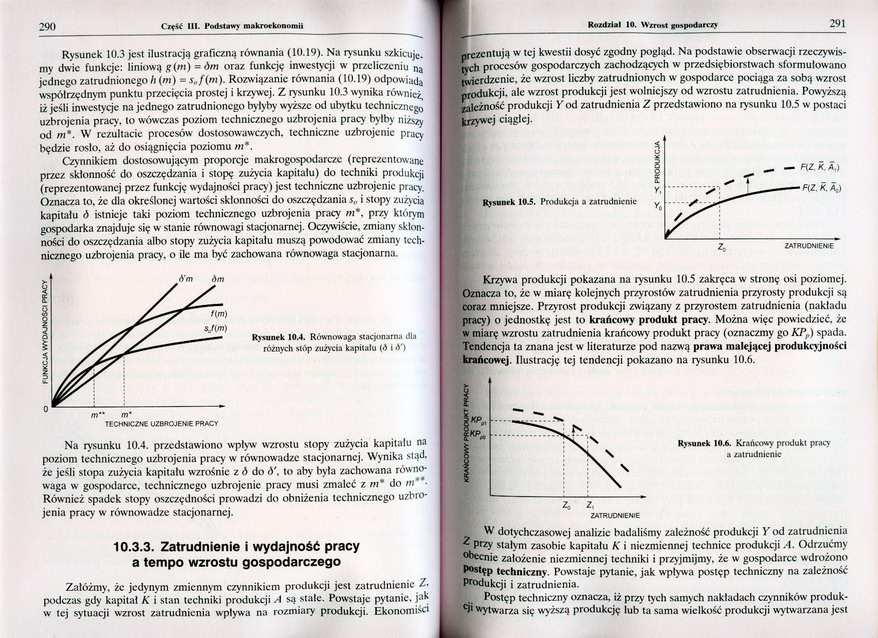
Rysunek 10.4. Równowaga stacjonarna dla różnych stóp zużycia kapitału (ó i A')

Na rysunku 10.4. przedstawiono wpływ wzrostu stopy zużycia kapitału na poziom technicznego uzbrojenia pracy w równowadze stacjonarnej. Wynika stąd. że jeśli stopa zużycia kapitału wzrośnie z A do ó'. to aby była zachowana rów nowaga w gospodarce, technicznego uzbrojenie pracy musi zmaleć z m* do /»**• Również spadek stopy oszczędności prowadzi do obniżenia technicznego uzbrojenia pracy w równowadze stacjonarnej.

10.3.3. Zatrudnienie i wydajność pracy a tempo wzrostu gospodarczego

Załóżmy, że jedynym zmiennym czynnikiem produkcji jest zatrudnienie podczas gdy kapitał K i stan techniki produkcji A są stale. Powstaje pytanie, jak w tej sytuacji wzrost zatrudnienia wpływa na rozmiary produkcji. Ekonomiści

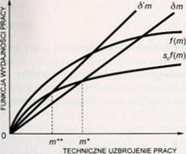
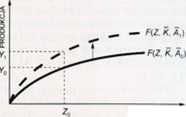
•zentują w tej kwestii dosyć zgodny pogląd. Na podstawie obserwacji rzeczywis-₍ch procesów gospodarczych zachodzących w przedsiębiorstwach sformułowano jerdzenie, że wzrost liczby zatrudnionych w gospodarce pociąga za sobą wzrost jdukcji. ale wzrost produkcji jest wolniejszy od wzrostu zatrudnienia. Powyższą leżność produkcji Y od zatrudnienia Z przedstawiono na rysunku 10.5 w postaci żywej ciągłej.

Rysunek 10.5. Produkcja a zatrudnienie

ZATRUOMENlf

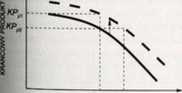
Krzywa produkcji pokazana na rysunku 10.5 zakręca w stronę osi poziomej. Oznacza to. że w miarę kolejnych przyrostów zatrudnienia przyrosty produkcji są coraz mniejsze. Przyrost produkcji związany z przyrostem zatrudnienia (nakładu pracy) o jednostkę jest to krańcowy produkt pracy. Można więc powiedzieć, że w miarę wzrostu zatrudnienia krańcowy produkt pracy (oznaczmy go KP_r) spada. Tendencja ta znana jest w literaturze pod nazwą prawa malejącej produkcyjności krańcowej. Ilustrację tej tendencji pokazano na rysunku 10.6.

Rysunek 10.6. Krańcowy produkt pracy a zatrudnienie

W dotychczasowej analizie badaliśmy zależność produkcji Y od zatrudnienia stałym zasobie kapitału K i niezmiennej technice produkcji A. Odrzućmy ^‘Cnic założenie niezmiennej techniki i przyjmijmy, że w gospodarce wdrożono techniczny. Powstaje pytanie, jak wpływa postęp techniczny na zależność Pfodu kej i i zatrudnienia.

.. Postęp techniczny oznacza, iż przy tych samych nakładach czynników produk-ty Wytwarza się wyższą produkcję lub ta sama wielkość produkcji wytwarzana jest