296 297 (8)

296

Czę<ć III. Podstawy makroekonomii

Rord/Jal 10. Wzrost gospodarczy

297

(10.32)

1 równania (10.32) wynika’, że tempo wzrostu dochodu narodowego - j zależy od stopy inwestycji (y) oraz efektywności inwestycji (*-J. Tempo wzrostu do-

I    /    1

chodu jest tym wyższe, im wyższe są — oraz —.

(10.32) znajduje się na rysunku 10.9 w położeniu oznaczonym g = i~. Wznosi ^s‘ę ona do góiy wraz ze wzrostem stopy inwestycji, co wynika z tego. że jej współ-

wzrostowi zasobu kapitału i jego efektywności (dochodzimy do tej formuły podob. nic jak w równaniu (10.23)). Możemy to zapisać następująco:

AY« AK e+Ae K+AK At.    (10.29)

Pomijając iloczyn AK ■ Ae (jest on bowiem stosunkowo mały) i dzieląc strona, mi równanie (10.29) przez równanie (10.27). otrzymujemy wzór na tempo wzrostu dochodu narodowego (przy założeniu, że w gospodarce stopa deprecjacji kapitału wynosi 0):

AY AK At

t"r^ł-    ^(l030>

Tempo wzrostu dochodu narodowego uzależnione jest więc od tempa wzrostu kapitału i tempa wzrostu jego efektywności. Tempo wzrostu kapitału zależy bezpośrednio od wzrostu inwestycji netto w gospodarce, natomiast zasadniczym czynnikiem wpływającym na tempo wzrostu efektywności kapitału jest dynamika postępu technicznego w gospodarce. Ze względu na to. iż w nowo budowanych obiektach wdraża się często nowe rozwiązania techniczne, dynamika inwestycji nic jest bez znaczenia dla dynamiki postępu technicznego w gospodarce.

Przyrost dochodu narodowego można też zapisać jako:

AV = /i.    (10.31)

k

gdzie: I - inwestycje (równe przyrostowi kapitału AK); — - współczynnik efektywności inwestycji |równy ~ lub j. określający przyrost dochodu narodowego przypadający na 1 jednostkę inwestycji (zakładamy stałość k).

Współczynnik efektywności inwestycji (|) występujący w równaniu (10.31)

jest odwrotnością krańcowego współczynnika kapłtałochłonności (k ) wskazującego. ile złotówek należy zainwestować w gospodarkę, aby w rezultacie dochód narodowy wzrósł o 1 złotówkę. Jeśli np. k = 2,5. to trzeba zainwestować 2.5 zl w celu uzyskania przyrostu dochodu narodowego o 1 zł w nowo zbudowanych obiektach. Dla uproszczenia pomijamy tutaj czas upływający od podjęcia inwestycji do przyrostu dochodu narodowego, zakładając, że obydwa procesy dokonują się w tym samym okresie.

W celu otrzymania wzoru na tempo wzrostu dochodu narodow ego podzielimy obie strony równania (10.31) przez Y. Mamy wówczas:

AY I 1

Y ^mYk’

udział inwestycji w dochodzie narodowym-

f Graficzną ilustrację formuły (10.32) przedstawiono na rysunku 10.9, gdzie na osi pionowej odłożono tempo wzrostu dochodu narodowego (oznaczając je symbolem g), na osi poziomej zaś stopę inwestycji (oznaczając ją symbolem i). Zauważmy, że równanie (10.32) można potraktować jako równanie linii prostej, gd/ic zmienną zależną jest tempo wzrostu dochodu narodowego, zmienną niezależną - stopa inwestycji, a współczynnikiem kierunkowym określającym kąt nachylenia prostej do osi poziomej - współczynnik efektywności inwestycji

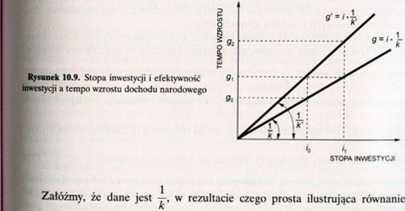
| czynnik kierunkowy, czyli —, jest dodatni. Podstawowy wniosek wynikający z iysun-

iku jest następujący: im wyższa stopa inwestycji, tym - przy innych czynnikach nic pienionych - wyższe tempo wzrostu dochodu narodowego. Przy stopie inwestycji

¹ Podobny formułę na tempo wzrostu gospodarczego, wzbogaceni) o jeszcze inne czynniki, inąl polski ekonomista Michał Kafceki (im-1970). Odnosił j* jednak do analizy gospodarki Minie planowanej i krajów słabiej rozwiniętych.