30 (559)

1.7. Prawdopodobieństwo klasyczne

Rzucając kostką, możemy otrzymać jeden z wyników należących do zbioru fi — {1,2,3,4,5,6}. Przyjmujemy, że kostka jest symetryczna (wszystkie wyniki pojawiają się równie często), zatem prawdopodobieństwo otrzymania któregokolwiek z wyników jest równe g. Rozpatrzmy zdarzenie polegające na wyrzuceniu parzystej liczby oczek. Zauważmy, że zdarzeniu temu sprzyjają trzy wyniki: 2, 4 i 6. Zatem prawdopodobieństwo tego zdarzenia jest równe | = 5.

Jeżeli wszystkie wyniki doświadczenia są jednakowo prawdopodobne (zdarzają się równie często), mówimy, że mamy do czynienia ze schematem (prawdopodobieństwem) klasycznym. W takiej sytuacji prawdopodobieństwo dowolnego zdarzenia A zawartego w przestrzeni fi określamy następująco:

DEFINICJA

Przykład 1

Jeżeli fi jest zbiorem skończonym i niepustym, to prawdopodobieństwem zdarzenia A C fi nazywamy liczbę:

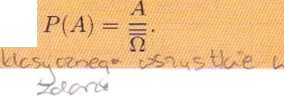
bjPj    riójr, i'€L

Oblicz prawdopodobieństwo otrzymania liczby oczek większej od 4 w jednokrotnym rzucie symetryczną kostką.

Przestrzeń zdarzeń elementarnych: fi = {1,2,3,4,5,6}, fi = 6. Zdarzenie polegające na tym, że wypadła liczba oczek większa od 4: A = {5,6}, A = 2. Zatem:    ₌

2

6

1

3'

Ćwiczenie 1

Rzucamy raz symetryczną kostką. Oblicz prawdopodobieństwo otrzymania liczby oczek: a) większej od 2, b) różnej od 5.    7    ■ '

Ćwiczenie 2    Z 7

Rzucamy trzy razy symetryczną monetą. Oblicz prawdopodobieństwo tego, że liczba otrzymanych orłów:

a) jest większa od liczby otrzymanych reszek,    b) jest nie większa od 3.

30    1. Rachunek prawdopodobieństwa