310 (22)

I

9 Obliczanie obwodu magnetycznego maszyn prądu

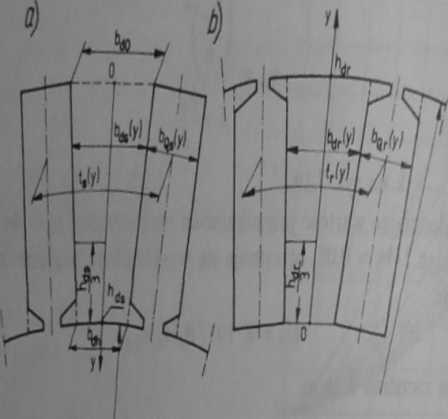
Rys. 9.17. Żłobek: a) stojana, b) wirnika—z oznaczeniami do obliczania napięcia magnetycznego

(9.42)

W przybliżeniu dla uzwojenia twomika współczynnik [7] ^T«rc = 0,015 + 0,0045/7

Przyjmując kierunek osi y od podstawy w kierunku głowicy zęba (zarówno w stojanic, jak i w wirniku) — rys. 9.17, można z wystarczającą dokładnością zmianę współczynnika t,_c(y) wyrazić za pomocą funkcji

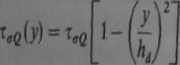
Zwykle wprowadzona poprawka uwzględniająca rozproszenie strumienia tylko nieznacznie wpływa na napięcie magnetyczne w zębie.

Szerokość zęba oblicza się ze wzorów:

— w przypadku stojana

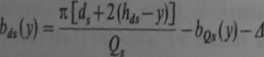
(9.44a)

— w przypadku wirnika

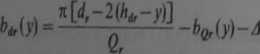
przy czym: A — naddatek technologiczny na szerokości wykrawanego żłobka, wg tabl. 4.6; Q„ Q,—liczby żłobków stojana oraz wirnika; pozostałe oznaczenia —jak na rys. 9.17.

Jeżeli indukcja maksymalna B_d(y) obliczona ze wzoru (9.41) jest większa niż ok. 1,8 T, to trzeba uwzględnić częściowe odciążanie zęba przez sąsiednie żłobki, kanały promieniowe w rdzeniu oraz przez izolację międzybłachową. Można przyjąć, że powierzchnie ekwipotencjalne w strefie zębowo-żłobkowej są cylindryczne, współśrodkowe z walcową powierzchnią rdzenia, a zatem, że

(9.44b)

0₁ tniecie magnetyczne w strefie zębowo-żlobkowej

311

natężenie pola magnetycznego w przekroju zęba jest takie samo, jak w przekroju żłobka leżącym na tej samej powierzchni ekwipotencjalnej. Strumień magnetyczny jednej podziałki żłobkowej rozdziela się więc wg równania

B_ttl. = BMb_t(y)l_r. = B,(y)My)/F«+/Wy)My)I/,+

+HoH_i{y)b_i{y){ 1 -k_fe)lł_p+n₀H_i(y)t{y)n„b_l,    (9.45)

w którym po prawej stronie składnik pierwszy wyraża strumień w stalowych częściach zęba, drugi — w żłobku, trzeci — w izolacji międzyblachowęj, czwarty zaś — w n_B promieniowych kanałach wentylacyjnych o szerokości b. Zależność między idealną indukcją w zębie obliczoną w założeniu, że cały strumień przechodzi tylko przez stalowe części zęba, a indukcją B_d rzeczywiście w nim występującą ma zatem postać

firf(y) =    (9.46a)

przy czym współczynnik odciążenia zęba

(9.46b)

_{k (v)=} W | l-^r« t(y)n_vb, m MlFe *f« b₄(y)l_F.

W równaniu (9.46a) występują dwie niewiadome: B_d(y) i ffjfy); do jego rozwiązania jest więc potrzebne jeszcze jedno równanie wiążące te wielkości. Równaniem tym jest zależność B = f{H\ tj. charakterystyka magnesowania zastosowanego ferromagnetyka. W projektowaniu wspomaganym komputerowo poszukiwanie niewiadomych funkcji oraz obliczanie całki (9.40) odbywa się za pomocą algorytmu opracowanego w założeniu warstwowej dyskrety-zacji zęba.

W przypadku zęba o prostym kształcie, np. o ściankach równoległych lub o zarysie trapezu (rys. 7.17) można indukcję B_d oraz natężenie pola H_d wyznaczyć wykreślnie przyjmując, że współczynnik odciążenia k₀ jest stały wzdłuż wysokości żłobka i ma wartość taką, jak w warstwie o największej indukcji w zębie. W tym celu, dla dowolnej wartości natężenia pola H — np. 1000 A/m — oblicza się składnik ft₀k₉H i okłada na wykresie charakterystyki magnesowania B = f(H) w dół od osi odciętej (rys. 9.18). Przez wyznaczony w ten sposób punkt A oraz przez początek układu współrzędnych prowadzi się prostą p, a następnie rysuje równoległą do niej prostą p' przechodzącą przez punkt odpowiadający indukcji B,_d. W punkcie P przecięcia prostej p' z charakterystyką magnesowania znajdują się rzeczywiście występujące wartości indukcji B_d oraz natężenia pola w zębie H_d. Obliczenia projektowe można usprawnić układając tablicę lub sporządzając dla danego gatunku blachy wykresy zależności B* - przy różnych wartościach współczynnika k, (rys. 9.19).

Napięcie magnetyczne w zębie U_d o prostym kształcie oblicza się z wystarczającą dokładnością ze wzoru

U* -    (9.47)