34 (523)

74 Przekształcenie Laplace'a

• Fakt 6.2.14 (różniczkowanie oryginału)

Jeśli funkcje f(i) i /'(<) są oryginałami oraz £ {/(()} = F(s), to

£{/'(<)} =sF(s)-/(0⁺),

gdzie /(0⁺) = lim /(<).

i—o+

O Ćwiczenie* 6.2.15

OO

Uzasadnić powyższy fakt.

Wskazówka. Do całki f    " dl zastosować wzór na całkowanie przez czyści.

o

• Wniosek 6.2.16 (n-krotne różniczkowanie oryginału)

Jeśli funkcje f(ł), f'(t), .... /⁽ⁿ⁾(0 oryginałami oraz £ {/(t)} = F(s), to £{/(">(<)} =

= sⁿF(s) - sⁿ"7 (0+) - s"-²/' (0⁺) + .. ■ - s/<"-²> (0+) -    (0+) ,

gdzie

/(0⁺)=_ilim/(l), /' (0+) = ₍lim f'(t)...../<»-O(₀+)₌Km /<■-«(*).

• Fakt 6.2.17 (całkowanie oryginału)

Jeśli funkcja /(() jest oryginałem i £ {/(*)} = F(s), to

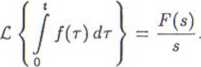
O Ćwiczenie* 6.2.18

Pokazać, że jeśli funkcja /(t) jest oryginałem, to również funkcja

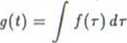
o

ma tę własność i to z tym samym wykładnikiem wzrostu co /(<). Następnie udowodnić

powyższy fakt korzystając ze wzoru na różniczkowanie oryginału.

• Twierdzenie 6.2.19 (holomorficzność i różniczkowanie transformaty)

Jeśli funkcja f(t) jest oryginałem, to jej transformata Laplace’a F(s) jest funkcją holomorficzną w pólptaszczyźnie Res > a, gdzie a jest wykładnikiem wzrostu oryginału f(t). Ponadto dla n 6 IV prawdziwa jest równość

(-l)ⁿ.F<")(s) = £{<"/(<)}.

O Ćwiczenie* 6.2.20

Wykazać, że jeśli funkcja /(() jest oryginałem, to dla dowolnego n 6 N funkcja (”/(() też jest oryginałem.

Fakt* 6.2.21 (całkowanie transformaty)

Jeśli funkcja jest oryginałem i £ {/(()} = f(s), to

= J'■» da,

gdzie

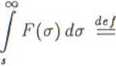
lim

Re p—oo

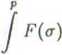
dc.

Ćwiczenie 6.2.22

Korzystając z własności przekształcenia Laplace’a wyznaczyć transformaty funkcji:

a) t ;	b) (^ne°‘;	c) t^2 coswł;	d) (sin uii
e) cos t — t sin t ;	f) J r^7e^iT dr\	g) J rsin2rdr;	h*) ^Sin2<
	0	0
^r> '7"^;	f sin T *> j —^dr-0	,.*r 1-cost ^k ' te^1

O

• Fakt 6.2.23 (transformata oryginału okresowego)

Jeśli f(t) jest oryginałem i w przedziale (0,oo) jest funkcją okresową o okresie T, to

F(s) =

F_t(s)

-j T *

1 — e

i

gdzie FY(s) = J f(i)e~’¹ dt.

O Ćwiczenie* 6.2.24

Wyprowadzić wzór podany w powyższym fakcie, oo    „ (* + i)T

Wskazówka, j f(t)e~" dt =    [    f[t)e~“ dt.

1    *=» Ł

O Ćwiczenie 6.2.25

Naszkicować podane oryginały i znaleźć ich transformaty: