95687

4.3 WŁASNOŚCI PRZEKSZTAŁCENIA LAPLACE A

Fakt 4.3.1 (zmiana skali)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej a> 0

L{f(ca)}= -f(-\

a \a)

gdzie F(s) oznacza obraz funkcji IR).

Fakt 4.3.2 (o różniczkowaniu obrazu)

Jeżeli funkcja f(t) jest orysinałem. to

L{l"f(0) =(-l)"F'"'(s).

gdzie F(s) oznacza obraz funkcji IR).

Fakt 4JJ (o przesunięciu argumentów obrazu)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej u € R

L{e^mf(t)> = F(s -a).

gdzie F(s) oznacza obraz funkcji IR).

Fakt 4.3.4 (o przesunięciu argumentów oryginału)

Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej r> 0

L{ l(t - l)f(t - X)} = e'^srF(s).

gdzie F(s) oznacza obraz funkcji (R).

Fakt 4.3.4 (o całkowaniu oryginału)

Jeżeli funkcja IR) jest oryginałem, to

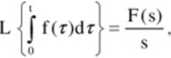
gdzie F(s) oznacza obraz funkcji IR).

Fakt 4.3.5 (transformaty ważniejszych hinkcji c.d.)

F^;unkcja	Transformata
shat	a
	2 2 s +a
chat	s
	s‘ +ar
t^ne“	n!
	(8-a)**'
e^sinyft	P
	(s-a)^2 + p^2
e^cos/*	s-a
	(s -af + fi^2

4.4 SPLOT FUNKCJI

Def. 4.4.1 (splot funkcji)

Niech funkcje IR) i g(t) będą całkowalne na każdym przedziale [O.T|. gdzie T > 0. Splot funkcji fR) i g(t) oznaczamy symbolem f(t)*g(t) i określamy wzorem