355 (7)

Ponieważ COS90* - O, sin90’-l. więc

Ctgl_A — Ctg- COS*.

Zamieniając funkcje wc wzorze na ich odwrotności, otrzymamy

tf*a-*f *•««*.    (a)

Z trójkąu Zn CG na podstawie wzoru cotangensów uzyskamy

ctg (IW —A) • sin 90* - ctgy - sin (ę-ar)-cos 90’ • cos (p-;r).

Ponieważ ctg(180*-/t) - -dgA, sin90’ - 1,    90° — 0. stąd    %    *

* ctg A • erg/-sin (?-.*).

Zamieniając funkcjo we wzorze na ich odwrotności, otrzymamy

-tg- tgy cosec(f-jr).    (b)

Za wzorów (a) i (b) obliczamy tgy, dostając odpowiednio:

	czyli	•gy- tg^-cosz;
sec*
	czyli	tgy - -igA • sin(p—ar)
cosec (g a^-)

Obie otrzymane wielkości przyrównujemy do siebie

tgr_A*coajr - —tg A • sin(f—x\

Skąd oUitec/nic

tg A - -tgt_x ct*x- cosec(g-or).    (1.34)

Z trójkąta Zn CG, stosując wzór cotangensów, otrzymujemy

ctg90* •tin<180"— A) - ctg(90’-A) • sin (o *)-cos(*-*)• cos(180*-,4),

a>U

0 - tg* s*n(g—ar)—cos(g—*) •(—cos^ś);

skąd ostatecznie

tg* - —Ctg(f—ar) • co* A.    (1J3)

Wzory (1.33)—(1.35) znalazły zastosowanie przy opracowaniu niektórych tablic służących do rozwiązywania trójkątów sferycznych, w tym także do obliczania wysokości i azymutów ciał (np. UM. 20. TN-64).

WYPROWADZENIE WZORÓW (2.1) I (2.2)

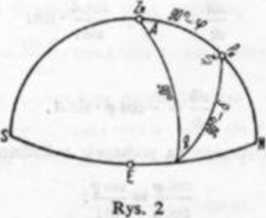
Wzór (2.1) wyprowadzamy za pomocą wzoru cosinus* boku, biorąc tu pod uwagę bok 90* 3

Cry» 2):

cos (90* 6) "• cos 90' * cos (90*— g) f sin 90* • słn (90* —p) • co* A.

555