36 (547)

Biblioteczka Opracowań Matematycznych

W dowolnym punkcie kola o promieniu a mogą pojawiać się punkty świetlne. Wyznaczyć wartość oczekiwaną oraz wariancję odległości od środka kola dla pojawiającego się punktu.

Rozwiązanie:

Odległość R pojawiającego się punktu świetlnego od środka koła można wyrazić przy pomocy x i y następująco:

Stąd:

R = yjx² + y²

R'

1_

na

i* u

^e(^r)=-~t UJ*² + y¹*# = ćj \^d*\^R'^dR = Ćp J

R'sa*

0 0

I

na

2x a

o_L3_Jo

dj = - \dt =

nr. 3

j

18

4

9

^D'W-fdł\

R <a~

0 0

95/ Dwuwymiarowa zmienna losowa (X, Y) ma gęstość daną wzorem: 1

/W)=

3Q0ny[ÓJ5

cxp

1,5

(.y-5)² _t (x-5)y _f jr

100

50

225

Wyznaczyć EZ oraz D² Z dla zmiennej losowej Z = aX + by. Rozwiązanie:

Rozkład podany w zadaniu to dwuwymiarowy rozkład normalny. Dwuwymiarowy rozkład normalny wyraża się wzorem ogólnym (1.41):

(1.41)

exp

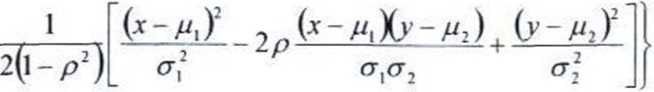
2n(J^CT₂yj\ - p‘

Z rozkładu podanego w zadaniu odczytujemy, że:

ll-^=0,75; p¹ — 0,25; |p| = 0,5; |p|<l.

<7,o. = 150; cr* = 100; o; - 225; —»• cr, = 10 o. = 15.

P, =5; Pi =0.

A zatem zmienna X ma rozkład N(5.10) a zmienna Y rozkład N(0,15). EZ = E(aX +by) = aEX + bEY = 5a

D Z = D²(aX + M')+ 2_P^^Y = 100a² + 225b² - 150a6

W zadaniu wykorzystano wzór (1.42):

(1.42) _D.f'_Xl.j_iD>x..±±_aMt„X_l)

•*J J

²⁵

96/ Dwuwymiarowa zmienna losowa (X, Y) ma rozkład o gęstości:

20/r

✓

a! Zbadać czy zmienne losowe X i Y są niezależne; b/Obliczyć P(-2<X<1;1<Y<3) c/ Obliczyć P[(X. Y) eD] gdzie:

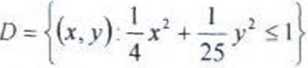
Rozwiązanie:

Z rozkładu zmiennej losowej (X,Y) odczytujemy, że:

1/ zmienne losowe X i Y sąnieskorelowane ponieważ p = 0;

2/ cr,(7₂ = 10 er,² = 4 er² = 25 czyli <r, = 2 cr₂ = 5

Mi = M₂ = 0

Zmienne losowe jednowymiarowe X i Y mają rozkłady normalne odpowiednio X~N(0, 2) oraz Y~N(0,5).

Funkcje gęstości dla zmiennych X i Y mają postać:

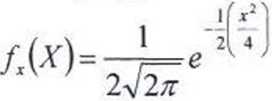
oraz

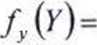
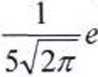
Dla każdego x,yeR zachodzi: f(x,y) =f_x(x) f_y (y) więc zmienne losowe X i Y są niezależne.

b/ P{- 2 < A < 1:1 < Y < 3)= P{- 2 < X < \)p(\ < Y < 3)= P

O

lP 0		f 1 3)
-1 < X. <	P
l 2 J		15 5 J

F

d

P[(X,rhD]=p\-_Ąx’+-,’tlj-Sj— Wprowadzamy nowe zmienne: x = 2rcos(f) y = 5rs\n<f>

Obliczamy jakobian przekształcenia: \j\ =

(F(0,6)- F(0,2)) = 0,5328 • 0,1464 = 0,078

' -KF-ś'¹).

dxdy

2 cos (p -2 r sin (/> 5sin0 5rcos0

= lOr

f 2x

C 2x

r«x,r)_e^D)- I |

\ o

10 rd<p

-Ir²

e ¹ rd<t>

\ o

dr = \-e ² * 0,3935

97/ Niech X i Y będą niezależnymi zmiennymi losowymi o tym samym rozkładzie normalnym N(m, a). Wyznaczyć współczynnik korelacji między zmiennymi U = a X + b-Y oraz V = aX - b-Y.

-71-