38 (521)

Biblioteczka Opracowań Matematycznych

EY=Yy,_Pi = 4.2:    f(>'^J) = £ V? P, = '7-8:    D¹ Y = e{y²)- (EY )² = 0.16.

1=1    /*1

E(XY)=Y.'L^x>’P* = l(4 0,2 + 5- 0,l)+ 2(4 -0.1 + 5 0)+ 3(4-0,5 + 5 - 0,l) = 9,6

i k

Cov(X,Y)= E{XY)~ EXEY = 9,6-9,66 = -0,06

= -0,16

Cov{X,Y) -0,06 ^P 4d²xŻJy 0.36

Uwaga! Współczynnik korelacji jest miarą współzależności liniowej zmiennych losowych Jeżeli współczynnik korelacji jest równy 0 to mówimy, że zmienne losowe są nieskorelowane. Jeżeli współczynnik korelacji jest równy 1 to znaczy, że jedna zmienna losowa jest funkcją liniową drugiej. Równanie prostej regresji Ii-go rodzaju zmiennej Y względem zmiennej X wyraża się wzorem (1.44):

(L44) y-EY x-EX

-= p-

Równanie prostej regresji Ii-go rodzaju zmiennej X względem zmiennej Y wyraża się wzorem (1.45):

(1.45) x-EX ₌ y-EY

^P °y

Stąd równania prostych regresji 11-go rodzaju odpowiednio: zmiennej Y względem zmiennej X oraz zmiennej X względem zmiennej Y mają postać:

^>~⁴— = -0,16 -~^2?3; --~-²-³ = -0.16 ^>;~⁴-0,4    0,4    0,9    0.4

100/ Dwuwymiarowa zmienna losowa (X, Y) ma rozkład normalny o parametrach: pi = 3, p₂ ⁼ A = 1,2; o₂ =0,8: p = 0,6.

Podać gęstość tego rozkładu oraz napisać równanie prostej regresji ll-go rodzaju zmiennej losowej X względem zmiennej losowej Y.

Rozwiązanie:

Dwuwymiarowy rozkład normalny wyraża się wzorem (1.41). Podstawiając do wzoru (1.41) wymienione w zadaniu parametry otrzymujemy gęstość dla

/(•*>>) =

i

1

1,536 n

exp

1.28

2tt -1,2-0,8-0.8

cxp

1.44

1	(x-3)^2 2-0,6 •(*-3)6-1) . (y-\Y 1
2 • 0,64	L (u)^2	1.2 0,8 ' (0.8)^2
(*-3)6-1), 6-tf 0,8 0,64		•

Równanie prostej regresji 11-go rodzaju wyznaczymy ze wzoru (1.45). Stąd podstawiając do wzoru (1.45) dane z zadania otrzymujemy:

^JC_3 =0,6^V_1

*-3 = 0.72

V-1

*-3 = 0.9(v-l).

1,2 ' 0.8 ' 0.8 101/ Dwuwymiarowa zmienna losowa (X, Y) ma rozkład nortfialny o gęstości:

/(Ar.^) = cexp|--

2 1 I 2

* *V + — V

2    4' JJ

Wyznaczyć stałą c oraz równanie linii regresji Ii-go rodzaju zmiennej Y wzgl. zmiennej X.

Rozwiązanie:

Funkcja f(x,y) jest gęstością dwuwymiarowego rozkładu normalnego. Poprzez przyrównanie do wzoru (1.41) odczytujemy niektóre parametry rozkładu a pozostałe obliczamy z odpowiednich zależności:

A zatem, odczytujemy, że: /// = /u₂ = 0.

Pozostałe parametry rozkładu w tym stałą c obliczamy:

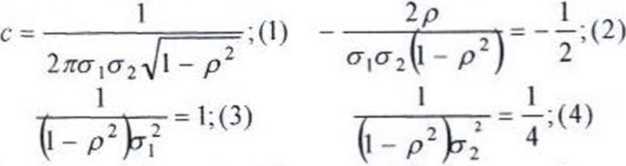
Dzieląc równania (3) przez (4) otrzymujemy zależność:

4 -»

f

= 4

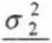
<T

2

1

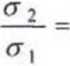
2

Dzieląc równania (3) przez (2) otrzymujemy zależność:

1    q,o-₂(l-p2)    a ₂ = 2

(l -p²)crt    -2 p    2pcj\

£ł _{= 2}

Wykorzystując poprzednio otrzymaną zależność _CT| “ otrzymujemy, że: (4p)²=4: 16p² = 4: p²=-^-; P = y-

= 1 —> <J, =

Wstawiając otrzymane p do zależności (3) i (4) obliczymy a, oraz a₂: l . 2-Jl    i l    4^3

D²

l-I

Wstawiając do (1) otrzymane wielkości obliczymy c: 1    3 JJ

c =

- 2-Ji 4V3

LIZ------

3    3

3

-75-