33 (661)

Biblioteczka Opracowań Matematycznych

Rozkład zmiennej Z zapisano w tabeli 56. Tabela 56.

Z	*» im	3	4	5	6	/ f
p	0,2	0,1	0,2	0,1	0,2	0,2

Wyznaczyć dystrybuantę dla zmiennej losowej Z. Gęstość zmiennej losowej Z ma postać:

6^2dla ^Je<°’^1>

/M=    ^y*^<0'^l>

0 d,a ^te<°’^1>

>’€< OJ >

Płaszczyznę X Y możemy podzielić na obszary tak jak to widać na rys 15.

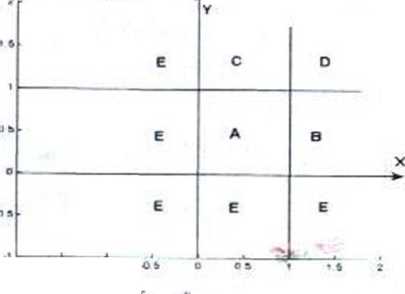
o o

Rys. 15 * ^{ł 1}

Dla (x,y) e A. F[x,y))=6^(x^{ly-yx-y²)dy)dx = x²y~{?>-x-y)

EZ = 10,2 + 3-0,1 + 4-0,2 + 5-0,1 + 6-0,2 + 7-0,2 = 4,4 (EZ)²= 19,36

E(Z²) = 4-0,2 + 9-0,1 + 16-0,2 + 25-0,1 + 36-0,2 + 49-0,2 = 24,4 D²Z = 24,4-19,36 = 5,04 86/ Dobrać stałą k tak, aby funkcja f(x.y)=> była gęstością dwuwymiarowej zmiennej losowej Z - (X, Y).

Rozwiązanie:

Aby funkcja f(x,y) była gęstością zmiennej losowej Z musi być spełniony warunek:    >/¹

.    V    0 < < 1

Jcx\{ 2-x-v) dla

’    0<y<\

xi< 0,1 >

0 dla

y<£< 0,1 >

^k\ \xy{2-x-vdy)

\0

o V o

= k

x²    X³    JC²

-ll

dx = 1

	2,2 3l	^1 \f 2
dx = k\ 7 o k ł >-7=i;	*y ^xy	' — * o II o	* *
	L 2 3 j k =6.		r 2 3 J

dx =

Dla (x,y) £ B: B(x,y) = 6 j Jxy(2 - x -y)dy dx = y²(2 - y)

o Vo    )

Dla (x, y) £ C:    F(x,y) = ó fj \(xy(2 -x~y))dy dx = x²(2-x)

<& = 1

Dla (x. y) e D: f(x,y) = 6 jj jxy(2    >)dv

o \0

Dla (x, y) eE: F(x,y) = O Dystrybuanta zmiennej losowej (X, Y) ma postać:

F(.v,v)=

0    dla innych :x,y x² (2 - x) dla 0 < x < 1; y > 1; y²(2-y) dla 0< v< 1; jc> 1;

x²y² (3 - ,v - v) dla 0 < * < 1; 0 < y < I;

dla xy>0 0 poza tym

1    dla x > 1; y > 1.

87/ Gęstość zmiennej losowej (X, Y) dana jest wzorem:    Axy)=

Obliczyć P(1<X<3; 2<Y<3).

Rozwiązanie:    1    .

P(\ < X < 3;2 < Y < 3)= J Jf(x,y)dy dx -    ‘ J\₂dx = J(-e ^(x*' +e ^(x,2))& =

l .2

₌ [_e t-3)__e-(- = )}; _=e 3(_e-3__e-2__e-._+|)

88/ Gęstość dwuwymiarowej zmiennej losowej (X, Y) dana jest wzorem:

f(x,y)=

6<T^(2x43>,) dla x > 0; y>0 0 poza

aJ Sprawdzić czy zmienne losowe XiY są niezależne.

Rozwiązanie:

Zmienne losowe X i Y będą niezależne jeżeli dla każdego x i y będzie spełniony warunek (1.37):

(1*37) f(x, y) =/_x (X) -f_y(Y)

Wyznaczamy rozkłady brzegowe dla zmiennych X i Y. Rozkład brzegowy dla zmiennej X wyznaczamy ze wzoru (1.38):

(U8)    /,(*)=]f{x,y)dy

-30

a dla zmiennej Y ze wzoru (1.39)

⁽⁰⁹⁾ /,(>')= \f{x,y)dx

-65-