34 (576)

Biblioteczka Opracowań Matematycznych

Dla zmiennych X i Y z zad 88/ otrzymujemy:

/,(*)= *\f(x,y)dy= j6e-^(J"’^vW = 6limJe^**^3l,4' = -21im[e    = -2jim(e -e ^;')=

„f	' 1	i'	1- ^2
"l	e^lx*^yk	e'\	) <>^2‘

Podobnie wyznaczamy rozkład brzegowy zmiennej losowej Y, otrzymując:

fp)= j/U>^=6p‘-Hfc=A

o    ^e

Ponieważ warunek (1.37) jest spełniony dla każdego x i y:

_6eA»*y) ₌ 2    3

e²’ e^,y

więc zmienne losowe X i Y są niezależne.

bł Wyznaczyć P(X< x/Y<y);

P{y < y)

X    X

= ^le ^lxdx = 2 je ^2xdx = 2

«*<’"<*>-AAr¹=    - * <*>- *)- j/.W* -

2x

-2x

= 1 -e

Jo

c/ WyznaczyćP(]<X<2,-l<y<l);

p( \<x < 2,-1 < Y < 0= P{\ < X < 2)r{-l< Y < l)= [F_r(2)- F_r(l)]-|f,(l)- F_t(o)J =

= f-<T⁴-M?~²] [l-e ³]

89/ Dla zmiennej losowej z przykładu 86/ wyznaczyć f(y/x) oraz dystrybuantę lego rozkładu warunkowego.

Rozwiązanie:

Gęstość rozkładu warunkowego określa wzór (1.40):

f(yi*)=

dla yeR

(1.40)    /W)

/,M

Wyznaczamy rozkład brzegowy zmiennej X:

<x    I

f_x(^x)= \6xy(l-x-y)dy = 6 jxy(2-x — y)dy - x(4- 3at) dla Jre(0,l)

-oc    0

Rozkład warunkowy zmiennej Y względem zmiennej X ma postać:

6xy{2 -x-y) ₌ 6y(2 -x- y)    ^

/(w*)=

.v(4 - 3*)    4 - 3x

0 dla xg(0.l)

' 1 '

Dystrybuanta rozkładu warunkowego ma postać: Hv^/jr)= J/(^v i x\tv = -jjj) \^^x'^v^^dv

Dla y — 0: F(y/x) = 0;    ,    .    6/-3^-2,■

Dla y e (0. I>:    ^fW'^H2-*-K» =-^-

DIay>l: F(y/x)=l.

90/ Wiadomo, że zmienne losowe X i Y są niezależne. Ich gęstości są odpowiednio równe:

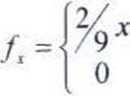
dla xe< 0,3 > dla x g < 0.3 >

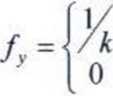
dla ye<Q.k > dla y£< 0,k >

Wyznaczyć rozkłady zmiennej losowej: Z\ = X Y;

Aby wyznaczyć rozkład zmiennej losowej Z\ korzystnie jest wyznaczyć dystry-buantę F(Z,):    f(z,)= F(x■ Y < Z,)= fj/(x)/(y}ixdy

D

Obszar D widoczny jest na rys. 16. Został on podzielony na dwa obszary:

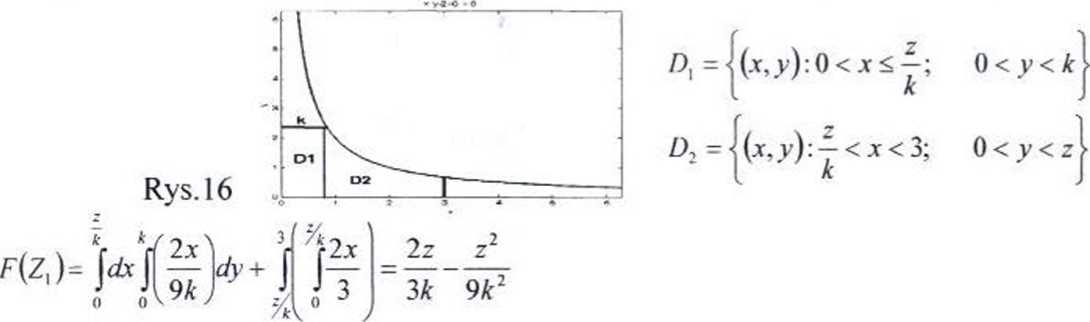
Dla Z>3kjest F(Zj) = L'_dF^

Stąd oraz ze wzoru: ^^z)⁼~dT otrzymujemy:

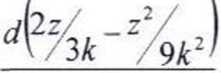
dz

/(Z,) = 0 dla z<£< 0,3k >

2    2 z

3    k 9k²

dla z e (0,3A >

91/ Niezależne zmienne losowe X i Y mają ten sam rozkład jednostajny w przedziale <0, 1>. Znaleźć gęstość prawdopodobieństwa zmiennej losowej Z = X+ Y. Rozwiązanie:

Gęstości zmiennych losowych odpowiednio X i Y oznaczmy jako f_x oraz/ .

0 dla x < 0 x > 1 1 dla x e< 0,1 >

Gdy zmienne losowe X i Y są niezależne gęstość rozkładu prawdopodobieństwa zmiennej losowej Z = X +Y wynosi: g(z) = g(x + y)

/,(*)=/,(*)=

-67-