341 (24)

(1)

10.7. Zasada równowartości energii kinetycznej i pracy

Popęd S siły sprężystości wyznaczymy z zasady pędu i popędu. Geometryczny przyrost pędu punktu materialnego w przedziale czasu (fi, *2) jest równy popędowi siły działającej na ten punkt w tym przedziale czasu, czyli

mv(T) - mv(0) = -5(0, 7*) + PT    (11)

Na podstawie równań (11) i (10) wyznaczamy

I® T) = PT + jy/2gN = P |V +

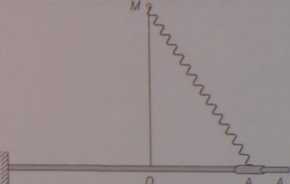
Suwak A o masie m może poruszać się bez tarcia wzdłuż prowadnicy AoD pod działaniem sprężyny o współczynniku sztywności c, zamocowanej w punkcie M (rys. 10.70). Wyznaczyć prędkość suwaka w chwili mijania punktu D, jeżeli w chwili początkowej miał on prędkość równą zeru i znajdował się w położeniu Aq, przy czym AoD = a. Przyjąć, że w chwili gdy suwak znajdzie się w położeniu £>, sprężyna jest nieodkształcona i jej długość MD = l.

ROZWIĄZANIE

Mamy do czynienia ze środkowym polem sił sprężystych, a więc z polem potencjalnym. Możemy więc napisać związek

W

gdzie przez jc oznaczyliśmy odkształcenie sprężyny, które będzie równe x = \fl² + a² — 1. Po podstawieniu do równania (1) i wykonaniu prostych przekształceń otrzymujemy

PRZYKŁAD 10.111

O    A A₀

RYS. 10.70_

vd — (Vl² +    ~

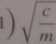
PRZYKŁAD 10.112

Ciężki pierścień A ślizga się bez tarcia po okręgu o promieniu R. Koło jest położone w płaszczyźnie pionowej xy. Na pierścień oprócz siły ciężkości działa siła sprężystości nici AOD. Stała sprężystości nici równa jest c. Znaleźć nacisk N pierścienia na okrąg jako funkcję kąta <p, jeżeli w chwili początkowej pierścień A znajdował się w położeniu równowagi chwiejnej Ao i został wytrącony z tego położenia z prędkością nieskończenie małą. W chwili gdy punkt A znajduje się * punkcie O, nitka jest nienapięta i jej długość równa się /, zaś w punkcie Aq jej długość wynosi 21 (rys. 10.71).