347 (19)

10.7. Zasada równowartości energii kinetyczne} i pracy .

347

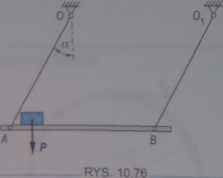
Belka AB o długości a jest podwieszona na dwóch równoległych nitkach O A = 0\B — l. Na belce w punkcie A spoczywa klocek o ciężarze P. Belka zostaje odciągnięta od położenia równowagi tak, że nitki tworzą z pionem kąt a, a następnie puszczona swobodnie. W chwili, gdy zajmie ona najniższe położenie, zostaje nagle zatrzymana, wtedy klocek zacznie przesuwać się po belce (rys. 10.76). Wyznaczyć współczynnik tarcia p. między belką a klockiem, aby klocek po osiągnięciu punktu B miał prędkość równą zeru.

Odpowiedź

/(I — cos a) a

Zadanie 10.117

Ciężar M o masie m może ślizgać się bez tarcia po pionowym pręcie AB, którego sztywność na rozciąganie jest równa ej. Koniec pręta B opiera się o śrubową sprężynę o współczynniku sztywności C2- Zaniedbując masę pręta i sprężyny, określić największe wydłużenie h pręta przy spadku ciężaru M z wysokości H bez prędkości początkowej. Przyjąć, że w chwili początkowej zarówno pręt, jak i sprężyna są nie-odkształcone (rys. 10.77).

Zadanie 10.118

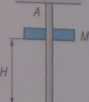
Odpowiedź mg

h =

c\ + c₂

!+,/! +

2H(ci 4- cg) mg

-RYS. 10.77.

Wahadło matematyczne o długości / znajduje się w położeniu Zadanie 10.119 równowagi. Jaką prędkość vo należy nadać kuleczce A, aby mogła ona krążyć po okręgu? Wyznaczyć także maksymalny naciąg nici (rys. 10.78).

Odpowiedź

m

' mg RYS. 10.78.

#0 > yftlg dla v = y/Slg Smaks ⁼ 6mg