343 (21)

343

10.7. Zasada równowartości onorgii kinetycznej i pracy...

Suwak A o ciężarze P nałożono na pierścień o promieniu R. W chwili początkowej prędkość suwaka równa jest zeru, a odległość AB == 2R. Znaleźć nacisk suwaka na pierścień w punkcie D, jeżeli wiadomo, że długość nieodkształ-conej sprężyny jest równa /?, a jej współczynnik sztywności c (rys. 10.72).

ROZWIĄZANIE

Na suwak w położeniu D działają następujące siły: ciężar P, reakcja pierścienia N, siła sprężyny S, siła bezwładności B(B_r, B_n).

Z warunku rzutów na kierunek n dostaniemy

N = P + B„ — S cos 45°    (1)

Siła sprężyny S = cx, gdzie x jest odkształceniem sprężyny x == R(Vl — 1). Siła bezwładności normalna B„ = P V²

=--, gdzie kwadrat prędkości wyznaczymy z zasady za-

g R

chowania energii

PRZYKŁAD 10.113

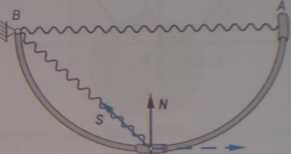
D, p    B_t

t^S"

RYS. 10.72

stąd

1 - 1 ₂ 1 -mgR + -cR — -mv + -cx ⁶ 2 2 2

mu² = 2PR + cR²[ 1 - (V2 - l)²] = = 2PR + 2cR²(V2- 1)

(2)

(3)

Po podstawieniu do (1) dostaniemy

N = 3P +2cR(V2- 1) - cR{V2 - 1)^ =

PRZYKŁAD 10.114

Punkt materialny o masie m spada pod wpływem siły ciężko

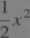
ści po powierzchni w kształcie paraboli o równaniu y ==

U i y mierzone w metrach). W chwili początkowej punkt znajdował się w położeniu A (4,8) i jego prędkość była równa zeru. Znaleźć maksymalny nacisk na powierzchnię (rys. 10.73).