442 2

442

II. Metoda Monte Car o i symulacja

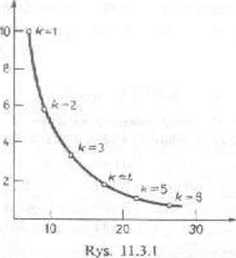
Z jednego eksperyment u (pary eksperymentów) nic można jednak wyciągać żadnych ostatecznych wniosków. Aby oprzeć się na solidnej podstawie statystycznej trzeba wykonać wiele eksperymentów; jest to potrzebne np. wtedy, gdy zamierza się zalecić pewną wartej k. Bailey wykonał 50 eksperymentów z 25 pacjentami w każdym i streścił związek miód czasem oczekiwania lekarza i pacjentów za pomocą krzywej z rys. 11.3.1.

Pojedyncze eksperymenty leż jednak mogą dać pożyteczne wskazówki co do planowania dalszych eksperymentów lub przybliżeń, jakie należałoby przyjąć w badaniu anab tycznym zadania. Użycie metod Monte Carlo na wielką skalę za pomocą komputerów wymaga starannego przygotowania. W przeciwnym razie możemy utonąć w morzu bezwartościowych wyników i ponieść wielkie koszty pracy maszyny. Trudno oczekiwać, żc metoda Monte Carlo - lub inne podobne eksperymenty - da wyniki bez uprzedniego zaplanowania. Trzeba zdecydować, jakie informacje chcemy otrzymać, jakie hipotezy chcemy sprawdzić, jakich kryteriów przerwania serii prób użyjemy. Często się to zaniedbuje; zwykle rozsądnie jest skonsultować się ze statystykiem.

Trzeba też pamiętać, że takie obliczenia opierają się na modelu rzeczywistości, a me na samej rzeczywistości. Odnosi się to w mniejszym lub większym stopniu do wszystkich zastosowań matematyki, ale jest szczególnie ważne, gdy obliczenia mają być podstawą jakichś ważnych decyzji. Dlatego jasne przedstawienie założeń poczynionych w modelu jest jedną z najważniejszych części raportu z badań matematycznych.

' Ze statystyki wiadomo, źe jeśli wykona się n niezależnych obserwacji pewnej wielkości, których odchylenie-standardowe jest równe <7, to błąd standardowy średniej tych obser wacji wynosi tr/yfn. W metodzie Monte Carlo, projektując eksperyment, można wpłyoS? na wartość a. Jeden z możliwych sposobów zilustrowano w poprzednim przykłada wykonanie eksperymentów dla ciągów przeciwnych liczb losowych i wyśredniowaflie wyników. Jeśli tym samym kosztem można wykonać dwa warianty eksperymentu, ¹ wyniki mają odchylenia standardowe <r, i rr₂ i jeśli te warianty powtarza się odpowiem z;, i n₂ razy. to jednakową dokładność otrzymuje się wtedy, gdy