436 2

436

11 Metoda Monte Car!o i symulacja

Ciąg (11.2.2) nazywamy przeciwnym względem wynikającego wprost z (11.2.1). Takłc^i^g są ważnym środkiem zmniejszania wariancji w przybliżeniach tworzonych metodą Monte ' Carlo: zob. § 11.3.

Przykład 11.2.2. Konstrukcja liczb losowych o danym rozkładzie dyskretnym. Przy. \ puśćmy, że zmienna losowa X przybiera wartości 0, 1 i 2 z prawdopodobieństwem równyia odpowiednio 0.18. 0.44 i 0.38. Ponieważ te prawdopodobieństwa mają po dwie cyfry po kropce, więc wystarczy - w obliczeniach ręcznych - używać dwucyfrowych sowych R o roz-kladzie prostokątnym.

Reguła:    R    X

O^R <0 18    0

0.18<R <0.62 I

0.62 < R < 1.00    2

Biorąc ?. (11.2.1) wartości 1007? otrzymujemy następującą tablicę:

55 69 30 29 45 81 72 34 35 88 81    35 07 63 02

„Y 121    11221    1221020

(Zauważmy, że powyższą regułę tak sformułowano, aby uniknąć wprowadzania poprawki do liczb losowych).

Definicja. Wyrażenie

P\_X<x)

oznacza prawdopodobieństwo tego. że zmienna losowa X przybiera wartość nie więfcśzfc od x.

Przykład 11.2.3. Ogólna metoda generowania liczb losowych o danej {ciągłej) dy& trybuancie F(x).

Reguła. Wziąć liczbę losową R o rozkładzie prostokątnym w przedziale [0. | i ^roZr . wiązać równanie F(X)- R. Wtedy X ma szukany rozkład i nazywa sic liczbą losową o dys-trybuancie F(x): zob. rys. 11.2.3.

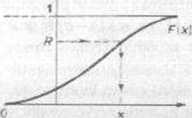
Rys. 11.2.3