433 2

Rozdział 11

Metoda Monte Carlo i symulacja 11.1. Wstęp

W większości zastosowań teorii prawdopodobieństwa formułuje się matematycznie pewne zadanie stochastyczne <tj. takie, w którym rolę odgrywa czynnik losowy) i rozwiązuje się je metodami analitycznymi lub numerycznymi. W metodzie Monte Carlo postępuje się odwrotnie: dane jest zadanie matematyczne i buduje się grę losową (liczbową), która w pewnym sensie prowadzi do tego zadania.

Rozwiązanie takiego zadania może być np. równoważne znalezieniu prawdopodobieństwa pewnego zdarzenia, albo wartości oczekiwanej lub dystrybuanty pewnej zmiennej występującej w grze. W każdym przypadku po skonstruowaniu gry lub doświadczenia, gra się w nią (powtarza się je) wielokrotnie, a otrzymane wyniki analizuje się tradycyjnymi metodami statystycznymi. Różne możliwości metody Monie Carlo zaczęto badać w latach czterdziestych naszego wieku.

Obrazowa nazwa metody stała się jednak tak popularna, że obecnie powyższe określenie jest zbyt wąskie. Na przykład w wielu zadaniach rozwiązywanych metodą Monte Carlo tkwi już pewien element przypadkowości w układzie luh procesie, który należy zbadać. Dlatego takie gry losowe można często uważać za symulację numeryczną najważniejszych aspektów układu (procesu). Kilka przykładów podamy niżej. ..Metody Monte Carlo^v w szerszym sensie były używane już w XIX w. (pobieranie próbek). Oto pewne dziedziny zastosowań tej metody:

(a) Zadania fizyki reaktorów i cząstek: np. neutron, ze względu na zderzenia z innymi cząsteczkami, musi poruszać się po losowej drodze: w rzadkich lecz ważnych przypadkach Patron może przechodzić przez warstwę materiału ekranującego (zob. rys. 11.1.1).

numeryczna

Sfronc

«v9wrwrrzna

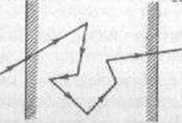
strono

gawnelrzr.a