5 (1709)

10.

1 punkt Funkcja / : M²

R ma w punkcie (1,1) obie pochodne cząstkowe

pierwszego rzędu równe 0.

(a)    / może ale nie musi mieć w tym punkcie ekstremum lokalne;

(b)    jeśli obie pochodne mieszane drugiego rzędu funkcji / zerują się w tym punkcie, a pochodne 0 oraz są w tym punkcie obie niezerowe, to / ma w tym punkcie ekstremum lokalne;

(c)    jeśli obie pochodne mieszane drugiego rzędu funkcji / w tym punkcie się zerują a 0(1,1) • 0(1,1) > 0, to / ma w tym punkcie ekstremum lokalne.

11.

12.

ma:

1 punkt I Podaj sens geometryczny gradientu funkcji.

ty pJI**

Ifif    ITu. kuinJę \7fCk)

⁶vt^ds>i sLojUha* C~y U4iJr.lv    ^HtfŁ /

LEr** k O* ^ ± <y Uf <?oLv*    f , J I

lienie początkowe ma rozwiązanie 1 ile ich ‘    u

/

X¹ = sin(t² + e¹); /    ^ /*W    ^

x(0) = l,    ^ ^ ^

/ r. t ^

3 punkty Czy poniższe zagadnienie początkowe ma rozwiąz?

gdzie x e [-100,100], t 6 [-100,100]. Uzasadnij posługując się twierdzeniami podanymi na wykładzie.    ,    btyhty

3-Od    ^x

~fb P'cavta,

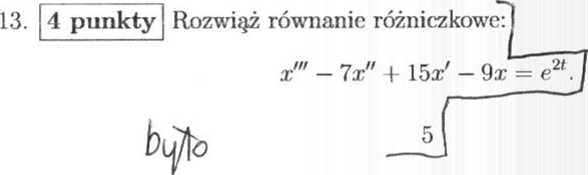
77/