5 (2119)

Biblioteczka Opracowań Matematycznych

P(X =-6) = P(III, III, III) = 0,001;

P(X = 10) = P(III, II, II) +P(II, II. III) + P(II, III, II) = 0,027;

P(X = 14) = P(I, II, III) + P(I, III, II) + P(II, I, III) + P(II, III, I) +P(III. II, I) + + P(III, I, II) = 0,108;

P(X = 18) = P(II, II. II) + P(III, I, I) + P(I, I, III) + P(I, III, I) = 0,135;

P(X = 22) = P(I, II, II) +P(II, II, I) + P(II, I II) = 0,162;

P(X = 26) = P(II, I, I) + P(I, I, II) + P(I, II, I) = 0,324;

P(X = 30) = P(i, I, I) = 0, 216.

Rozkład prawdopodobieństwa dla zmiennej losowej X można przedstawić w poniższej tabeli:

Xi	6	-	6	10	14	1S	22	26	30
Pi	0,001	0,009	0.018	0,027	0,108	0,135	0.162	0,324	0,216	Z* = i i

Tabela 3.

3/ Doświadczenie polega na pięciokrotnym rzucie monetą. Niech zmienna losowa oznacza stosunek ilości otrzymanych orłów do ilości otrzymanych reszek. Znaleźć rozkład prawdopodobieństwa tej zmiennej losowej.

Rozwiązanie:

Zmienna losowa X opisana w zadaniu 3/jest skokowa. Punkty skokowe to liczby określające stosunek ilości otrzymanych orłów do ilości reszek w pięciu rzutach monetą. Pomocniczo zapiszmy więc kolejne przypadki:

[o? r] = [1, 4] -> X] = %;    I

[o, r] = [2, 3]    x₂ = K ;    j

[o,r] = [3,2]->x₃=K;

[o, r] = [4, 1] X4 = 4;

[o, r] = [5, 0] -» x₅ = oo;

[o, r] = [0, 5]->x<i=0.

Ponieważ prawdopodobieństwa otrzymania orła lub reszki są równe 14 więc:

P(;c = 4) =

⁵Yi

4 12

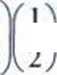
-'4, ^⁼⁰⁾⁼

o

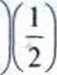
32.

= — P( :r = oo) = 32,

Ostatecznie rozkład prawdopodobieństwa zmiennej losowej X zapiszmy w tabeli 4:

Tabela 4.

X,	0	X	A	A	A	00
Pi	Vi2	Vi2	%	^l%2	Vb2	%2	2>.« ^1 i

4/ Dośw iadczenie polega na sprawdzaniu poprawności działania przyrządów w pięciu niezależnych próbach. Kolejny przyrząd sprawdzamy dopiero wtedy gdy poprzednia próba zakończyła się pomyślnie. Niech zmienna losowa oznacza liczbę sprawdzanych przyrządów, przy czym prawdopodobieństwo pomyślnego przejścia do sprawdzania kolejnego przyrządu wynosi 0,9. Napisać rozkład opisanej zmiennej losowej.

Rozwiązanie:

Opisana zmienna losowa X jest skokowa. Punkty skokowe to liczby oznaczające liczbę sprawdzonych podczas kontroli przyrządów. Stąd:

Xj= {1,2, 3, 4, 5}. Prawdopodobieństwa dla poszczególnych wartości zmiennej losowej X są równe:

P(X=1) = 0,1;

P(X = 2) = 0,9 • 0,1 = 0,09;

P(X = 3) = 0,9 • 0,9 • 0,1 =0,081;

P(X = 4) = 0,9 • 0,9 • 0,9 • 0,1 = 0, 0729;

P(X = 5) = (0,9)⁴= 0. 6561.

(Przykładowo, jeżeli zmienna losowa X = 3, to musiały wystąpić chipie pozytywne próby a trzecia zakończona niepowodzeniem)

Otrzymany rozkład zapiszemy w tabeli następująco:

Xi	1	2	3	4	5
Pi	OT	0,09	0.0S1	0.0~29	0,6561	it cC W-

Tabela 5.

5/ Do wyrobu takich samych elementów używa się pewnych półfabrykatów.

W magazynie jest n półfabrykatów. Prawdopodobieństwo wytworzenia z półfabrykatu dobrego elementu wynosi p. Niech zmienną losową będzie liczba półfabrykatów użytych do wytworzenia pierwszego dobrego elementu. Napisać jej rozkład.

Rozwiązanie:

Jeżeli przyjmiemy, że k -ty element wytworzony będzie dobry tzn., że wykorzystano (k-1) półfabrykatów po czym nastąpił sukces i wytworzono dobry element. Osiągnięto zatem k-1 porażek i 1 sukces. Stąd prawdopodobieństwo takiego zdarzenia wynosi:

P(X)=p-q^k'' dla 1 <k <n-l;

W przypadku gdy dobry element wytworzono dopiero za n-tym razem, czyli było n-1 porażek prawdopodobieństwo takiego zdarzenia wynosi:

P(X) =qⁿ-‘ dla k = n.

-9-