6

234
XI. Algebra macierzy
Dopełnienie algebraiczne- Mik określa się następującym wzorem:
Mik = (-1 )i+k-mik.
Przykład. Dana jest macierz A. Obliczyć minor mn oraz dopełnienie algebraiczne Alu. ...
Mamy
|
'2 4 3 |
2 4 3- | |
|
13 5 |
II |
1 3 5 |
|
4 2 1 |
4 2 1 |
3 5
= 2 1

(jest to minor dla. elementu an = 2).
Dopełnienie algebraicznemu =n(Wl)l+ł-mu = —7.
Utworzenie minor a dla dowolnej macierzy (nie kwadratowej) polega, na' wykreśleniu dowolnej ilości wierszy i kolumn, tak aby~eiementy nie-“wykreślone tworzyły macierz kwadratową p-tego stopnia. Wyznacznik PeJ macierzy jestlrnnbrem p-tegćTstopnia. *" ~
Przykład. Dana jest macierz
|
"3 |
2 |
1 |
4 | |
|
B = |
1 |
5 |
2 |
1 |
|
2 |
0 |
2 |
1 |
Obliczyć jej dowolny minor pierwszego, drugiego i trzeciego stopnia.
Wykreślając dwa pierwsze wiersze i trzy ostatnie kolumny otrzymamy minor pierwszego stopnia: tox = 2.
Wykreślając ostatni wiersz i dwie ostatnie kolumny otrzymamy macierz kwadratową drugiego stopnia, a wyznacznik tej macierzy jest minorem drugiego stopnia:
3
1
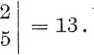
to2
Wykreślając zaś trzecią kolumnę otrzymamy macierz kwadratową trzeciego stopnia, a wyznacznik tej macierzy jest minorem trzeciego stopnia:
|
3 |
2 |
4 |
|
1 |
5 |
1 |
|
2 |
0 |
1 |
Rząd macierzy
-23.
ISi aj wyższy stopień minora o wartości różnej od zera nazywa się rzęctem danej fereśłbniUrzęclu macierzy ma szerokie^zastosowanie
przy badaniu układów równań liniowych.
Wyszukiwarka
Podobne podstrony:
OMiUP t1 Gorski02 Objętość porów określa się następująco: najpierw oblicza się geometryczną objętość
230 XI. Algebra macierzy Macierz kwadratowa, w której wszystkie elementy na głównej przekątnej są
236 XI. Algebra macierzy Zatem 2. Obliczenie wartości wyznacznika
232 XI. Algebra macierzy Mnożenie macierzy wykonuje się przez sumomnożenie wierszy pierwszej macierz
MATEMATYKA 3. MACIERZE I WYZNACZNIKI Rozwiązanie 3.11 Skonstruujemy macierz dopełnień algebraicznych
Wzory - matematyka kolokwium I Macierze i+ k • Dopełnienie algebraiczne : A^ = (- 1) Mlk dla% = 1,4.
Wzory - matematyka kolokwium I Macierze i+ k • Dopełnienie algebraiczne : A^ = (- 1) Mlk dla% = 1,4.
A~x - p-r • A° A° - transponowana macierz dopełnień algebraicznych macierzy AA 2 7
17 1.1. STRUKTURY ALGEBRAICZNE PROSTE określamy mianem homomorfizmu kanonicznego grupy G w jej grupę
Algebra dwuelementowa Określamy zbipt«P={0, 1}, przy czym 0*1. Operatory:
algebra koło4 1. Określić liczbę rozwiązań następującego układu równań w zależności od parametru p.
algebra koło6 1. Określić liczbę rozwiązań następującego układu równań wr zależności od parametru p.
algebra koło7 1. Określić liczbę rozwiązań następującego układu równań w zależności od parametru p.
page0242 234 Sekeyje Koniczne — Seklucyan a i b mają znaczenie wyżej określone. Z
Politechnika Wrocławska• Uktad równań:• Oznaczenie: vij=clj(xi)InterpolacjaZapis macierzowy ao%
Algebra relacyjna Algebrę ralacyjną stosuje się do zbiorów krotek czyli relacji, jednakże w
więcej podobnych podstron