7 (1827)

Biblioteczka Opracowań Matematycznych

c/ Wyznaczyć dwoma sposobami P(X = 2); P(X = 3); P(X < 2); P(X <-2); P(X > 0,1); P(-l <X < 3).

Rozwiązanie:

a/

W każdym rozkładzie suma prawdopodobieństw musi być równa 1 zgodnie z (1.1). A zatem aby wyznaczyć stałą k wystarczy odjąć od 1 sumę pozostałych prawdopodobieństw. Otrzymujemy wówczas, że k = 0,1. b/ Dystrybuantę dla zmiennej losowej X przedstawiono w tabeli 10:

Xi	(-od,-3>	(-3,-l>	(-1:0,1>		a.4>	<4,5>	(5,+oo)
f(x;	i o	0.05	0.2	0.5	0,6	0,9	1

Tabela 10.

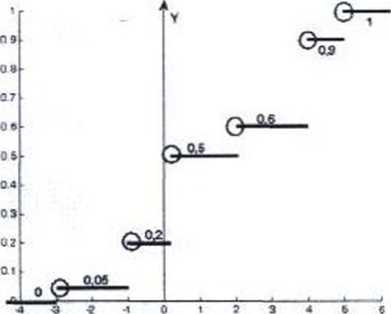
d Wartości prawdopodobieństw można obliczać przy pomocy funkcji prawdopodobieństwa lub z wykorzystaniem dystrybuanty.

Wykorzystując funkcję prawdopodobieństwa otrzymujemy:

P(X = 2) = 0,1; (odczytano z tabeli 9)

P(X = 3) = 0; (odczytano z tabeli 9, x = 3 nie jest punktem skokowym)

P(X < 2) = YA^X=) = P(X = -3)+P(X=-1)+ P(X = 0,1)=0,05+0,15+0,3 = 0,5 <2 __₍

P(X < -2) = £ P(X =*,) = />(* =-3) = p, = 0,05;

P(X > 0,1) = ^P(X = jf,) = P(X = 0,1) + P(X = 2) + P(X = 4) + P(X = 5) = 0,8;

x,20.l

P(-\< X < 3) = £P(X = *,) = P(X = -l) + P(X = 0,1) + P(X = 2) = 0,15+0,3 + 0,1 = 0.55.

-l<x,<3

Wykorzystując funkcję dvstrybuantv otrzymujemy:

P(X = 2) = F(2+0) - F(2) = 0,6 -0,5 = 0,1;

P(X = 3) = F(3+0) - F(3) = 0,6 - 0,6 = 0;

-12-

P(X<2) = F(2) = 0,5;

P(X<-2) = F(-2) = 0,05;

P(X>0,1) = P(0,1 < X < co) = F(co) - F(0,1) = 1-0,2 = 0,8:

✓

(Prawdopodobieństwa otrzymane dowolnym sposobem są takie same)

91 Wiedząc, że dystrybuanta zmiennej losowej Xjest określona następująco. Tabela 11.

Xi	(-CO.-1 >	(1.0>	(0,2>	(2.10*	(LO.+co)
FU)	0	03	0,7	0.75	1

P(-l < X < 3) = F(3)- F(-l) = 0,6 - 0,05 = 0,55;

wyznaczyć funkcję prawdopodobieństwa tej zmiennej losowej.

Rozwiązanie:

Punkty skokowe dystrybuanty to x,={-l, 0, 2, 10}. p, = P(X = -1) = F(-l+0) - F(-l) = 0,3 - 0 = 0,3; p₂ = P(X = 0) = F(0+0) - F(0) = 0,7 - 0,3 = 0,4; p₃ = P(X = 2) = F(2+0) - F(2) = 0,75 - 0,7 = 0,05; p₄ = P(X = 10) = F( 10+0) - F(10) = 1 - 0,75 = 0,25.

Tabela 12.

Xi	(-CD,-1>	(1.0>	(0.2>	(2,10*	(10.4X30)
F(x>	0	0.3	0.7	i - o	1

przedstawiono w tabeli 12

10/ W tabeli 13 dana jest dystrybuanta zmiennej losowej Y. Obliczyć przy pomocy dystrybuanty prawdopodobieństwa: P(Y<3,5); P(Y >0); P(l< Y <2'): P(-4 <Y<2); P(0<Y< 3).

Tabela 13.

Y	(-co,-5>	(-5.-2 >	(-2,1>	(1,3>	(3.+oo)
F(Y)	0	0.2	0,4	0.6	1

P(Y < 3,5) = F(3,5 + 0) = 1;

P(Y > 0) = P(0 < Y< co) = F(co) - F(0) = 1 - 0,4 = 0,6;

P( 1 < Y < 2) = F(2+0) - F(l+0) = 0,6 - 0,6 = 0;

P(-4 < Y < 2) = F(2+0) - F(-4) = 0,6 - 0,2 = 0,4;

P(0 < Y <3) - F(3) - F(0+0) = 0,6 - 0,4 = 0,2.

11/ Zmienna losowa X ma rozkład prawdopodobieństwa podany w tabeli 14:

Xi	_2	-1	0	i
Pi	0.3	0.1	0.2	0,1	0.3