86 (58)

'¹ /&})

1 /= I

Rys. 2.8

i

j

I

Analityczne postaci funkcji gęstości i dystrybuanty zmiennych losowych

O

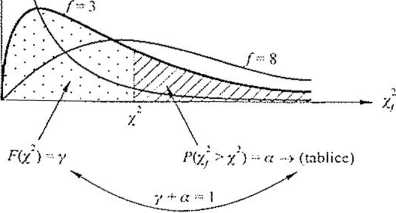
o rozkładach %j i gamma można znaleźć w literaturze przedmiotu, np. (Baran 1999).

Rozkład Studenta

Jeśli zmienno Xj. X₂.--; X ,• są wzajemnie niezależne i mają rozkłady normalne NfO; aj, to zmienna losowa

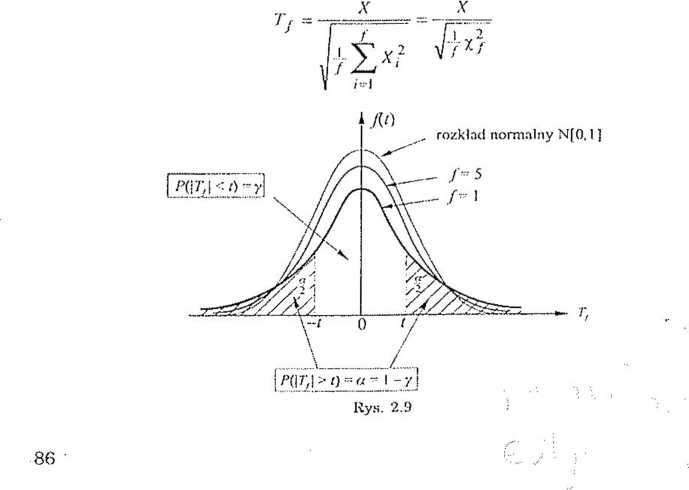
j

ma rozkład Studenta o /‘stopniach swobody. Do celów praktycznych tablicowane są wartości t, dla których    j > /)= a (tab. III). Wobec tego, jeśli

F(t) - P(Tf </), to (rys. 2.9)

/.•(,) = l-~.t/’(:r_n>/)    (2.17)

Uwaga: jeśli /> 30, to rozkład Studenta można z wystarczającą dokładnością zastąpić rozkładem normalnym N[0; lj.

2.1.3. Parametry opisowe zmiennej losowej

Ogólne własności zmiennych losowych o ustalonych rozkładach prawdopodobieństw mogą być przedstawiane za pomocą pewnych charakterystyk liczbowych nazywanych parametrami opisowymi. Parametry opisowe zmiennych losowych (w geodezji : wyników pomiarów) mają szczególne znaczenie, i to nie tylko teoretyczne.

Podstawowe parametry opisowe

Do podstawowych parametrów opisowych zmiennej losowej X można zaliczyć wartość oczekiwaną E(X), wariancję V(X) oraz odchylenie standardowe a^r.

parametry opisowe

wariancja:

wartość oczekiwana: E(X)

V(X)=b{[X-E(X)]²}

<- zmienna ciągła ~*

V(X)=] Ł =	r[x;-E(X)fPl = 1
4- co V(X)= Jj OC	x~ E(X)f f(x)dx

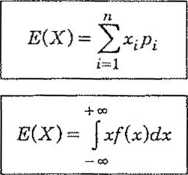
zmienna skokowa

odchylenie standardowe

a _x =    JVXX)

87