CCF20140115019

/ Kielan Turnau

wykształcenia uczniów daleko cenniejsze, niż opanowanie schematów rozwiązywania zadań na porównywanie różnicowe i ilorazowe.

Metoda analityczno-syntetyczna polega na kilkakrotnym przechodzeniu od analizy do syntezy i od syntezy do analizy. Odnosi się do zadań trudniejszych, jakimi nie będziemy się tu zajmować.

Pojęcie metody rozwiązywania zawęziliśmy tu celowo żądaniem, by prowadziła do odkrycia sposobu rozwiązania. Często jednak przez metodę rozwiązywania rozumie się metodę poszukiwania samego rozwiązania, z pominięciem sposobu. Rozróżnienie to jest bardzo istotne. Zauważmy bowiem, że w tym drugim rozumieniu metodą rozwiązywania jest też „mądre” zgadywanie. Zilustrujemy to postępowanie także na przykładzie zadania (9).

Zaczynamy od próby odgadnięcia rozwiązania: może sprzedano 20 kompletów? Następnie sprawdzamy, czy odgadnęliśmy dobrze: razem musiałoby być wówczas 33 komplety, a więc 198 (tj. 33-6) chustek. Było jednak 300 chustek, musiano więc sprzedać dużo więcej. Poprawiamy hipotezę: może sprzedano 40 kompletów? Byłoby wtedy razem 53 komplety, tj. 318 chustek. O 18, tj. o 3 komplety więcej niż w rzeczywistości. A więc sprzedano nie 40, ale 37 kompletów.

Jest to postępowanie nie tylko zupełnie poprawne, ale też bodaj najbardziej efektywne, o ile rozwiązujący dysponuje kalkulatorem umożliwiającym błyskawiczne wykonywanie mnożeń. Nie wymaga ono bowiem namysłu ani poszukiwań, szybko i niezawodnie prowadzi do celu. Tak właśnie rozwiązuje się w dobie komputerów wiele problemów praktycznych, tak skomplikowanych, że poszukiwanie sposobu rozwiązania, tj. ciągu działań byłoby bardzo żmudne, jeżeli nie beznadziejne. Jak najbardziej właściwe będzie więc pokazanie uczniom i tej drogi dochodzenia do wyniku, najlepiej w przypadku zadań trudniejszych, gdzie znalezienie sposobu rozwiązania przekracza możliwości większości uczniów.

Zgadywanie, nawet „mądre” ma jednak szereg wad, z których najistotniejszą jest niemożność jego uggólnignia,. Podczas gdy sposób rozwiązania może być łatwo uogólniony i zastosowany do innych podobnych zadań, rozwiązanie jakiegoś zadania metodą odgadywania i stopniowego poprawiania wyniku nie pomaga w sposób istotny w rozwiązaniu podobnego zadania zawierającego inne dane. Nie ma też ono większej wartości dydaktycznej, nie przyczynia się bowiem do kształcenia metod heurystycznych — jednego z głównych celów nauczania matematyki, a w szczególności celu rozwiązywania zadań przez uczniów. Z tych względów metody dochodzenia do sposobu rozwiązania, ocena różnych sposobów rozwiązania tego samego zadania, porównywanie sposobów rozwiązania różnych zadań, a potem ich uogólnianie znajdować się powinny w centrum uwagi nauczyciela podczas lekcji poświęconych zadaniom tekstowym.

7.6.7.    Metodyka nauczania rozwiązywania zadań tekstowych

Praca nad zadaniem rozpoczynać się powinna zawsze od rozbioru zadania. Termin ten zaczerpnęliśmy z metodyki nauczania składni, gdyż zachodzi tu daleko idąca analogia. Rozbiór zadania polega mianowicie na

wyodrębnieniu jego części składowych istotnych dla poszukiwania sposobu rozwiązania. Są to:

1)    niewiadome, których dotyczy pytanie lub polecenie zadania, oraz inne niewiadome występujące w zadaniu,

2)    dane,

3)    związki między niewiadomymi i danymi.

Rozbiór zadania wymaga odczytywania jego tekstu nie „za porządkiem”, ale w dyktowanej potrzebą kolejności. Najpierw więc uczeń odszukuje pytanie lub polecenie zadania (zazwyczaj, choć nie zawsze, znajdujące się na końcu), a w nim — niewiadome. Następnie przeszukuje tekst zadania, wyławiając z niego wszystkie dane oraz •— ewentualnie — niewiadome, o których nie było mowy w pytaniu, wreszcie fragmenty mówiące o związkach między niewiadomymi oraz między niewiadomymi i danymi. Rozbiór zadania trwa do momentu, gdy wszystkie potrzebne jego składniki zdają się być znalezione; często jednak bywa, że ukryte związki między niewiadomymi i danymi są ujawniane dopiero w dalszym etapie pracy.

Rys. 3 Rys. 4

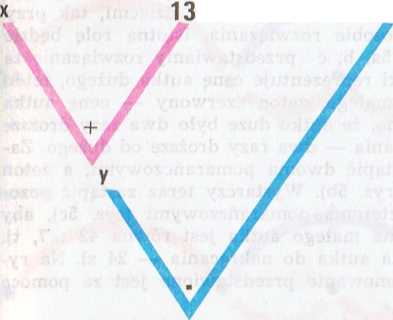
Nie warto zapisywać słowami znaczenia występujących w zadaniu liczb, a także znalezionych związków między nimi i niewiadomymi. Znacznie korzystniejsze będzie posłużenie sę w tym celu schematem graficznym, który przy tym często ułatwia znalezienie sposobu rozwiązania. Posłużmy się raz jeszcze zadaniem (9) jako przykładem. Oznaczywszy liczbę sprzedanych kompletów przez x, liczbę zaś wszystkich kompletów przez y, możemy wynik rozbioru zadania przedstawić drzewem (rys. 3) lub grafem strzałkowym (rys. 4). Pierwszy schemat bardzo ułatwi poszukiwanie sposobu rozwiązania drogą analizy, drugi zaś od razu dostarcza tego sposobu przez odwrócenie obydwu strzałek i oznaczonych nimi działań.

Drzewa i grafy strzałkowe stanowią dogodne, operatywne i bardzo uniwersalne rodzaje takich schematów i należy uczniów zachęcać do

Rys. 3    Rys, 4

6

m

300