CCF20140115004

Stefan Turnau

08_/

W przekonaniu znacznej liczby ludzi, zastosowania matematyki występują tylko w dwu poziomach:

1)    elementarnej arytmetyki liczb dziesiętnych, potrzebnej rzeczywiście każdemu i stosowanej na co dzień przez wszystkich, bez względu na poziom wykształcenia,

2)    matematyki wyższej, niedostępnej dla większości, stosowanej przez ludzi nauki i techniki z wyższym wykształceniem i tylko w badaniach naukowych lub projektowaniu rozwiązań technicznych, architektonicznych itp. Zgodnie z tym przekonaniem, wiedza matematyczna nabyta w szkole podstawowej i średniej, choć może i przyczynia się do kształcenia umysłu, nie ma jednak niemal żadnych zastosowań praktycznych.

Poglądowi temu, niestety, trudno odmówić sporej dozy słuszności. Wynika to jednak nie z rzeczywistej bezużyteczności matematyki, ale z wad jej nauczania. Większość ludzi, rzeczywiście, poza arytmetyką nie stosuje niemal nigdy matematyki w swej codziennej działalności, nie dlatego jednak, że matematyki zastosować się w tej działalności nie da, ale dlatego, że ludzie ci nie zostali do tego przygotowani przez szkołę i nawet wyobrazić sobie nie mogą, na czym te zastosowania mogłyby polegać.

Aby lepiej zrozumieć, co znaczy stosować wiedzę i metody matematyczne, czego więc powinniśmy uczyć w szkole, przypatrzmy się dwom sytuacjom, których bohaterowie mogliby posłużyć się matematyką, znacznie ułatwiając sobie i innym pracę, gdyby umieli i chcieli to zrobić.

f_; Aptekarka oblicza należność za 20 proszków według recepty. Znajduje jwąrtość każdego specyfiku, mnożąc jego cenę (znalezioną w cenniku) iprzez wskazaną na recepcie ilość specyfiku przypadającą na 1 proszek i przez 20. Dobiega już końca, gdy orientuje się, że proszków tych ma być nie 20 — jak jej się zdawało — ale 30. Skreśla więc cały dotychczas wykonany rachunek i zaczyna go od początku.

Czy takie postępowanie pani magister jest racjonalne? Gdyby zastanowiła się w momencie zauważenia pomyłki, jak najszybciej ją skorygować, wykorzystując wykonaną już pracę, mogłaby znaleźć rozwiązanie następujące. Wartość 30 proszków, to 3/2 wartości 20 proszków. Skoro wartość 20 proszków została obliczona, należy otrzymaną liczbę zwiększyć o 50%, tzn. na przykład podzielić przez 2 i wynik dodać do pierwszej liczby.

Do jakich wiadomości z matematyki odwołuje się to rozumowanie? Korzystamy tu z proporcjonalności wartości leku do jego ilości; w tym celu trzeba wiedzieć, jak znaleźć współczynnik tej proporcjonalności, oraz wiedzieć, że dla otrzymania nowej wartości należy pierwotną wartość pomnożyć przez ten współczynnik. Korzystamy więc z zupełnie określonej wiedzy matematycznej. Przy tym — co jest jeszcze istotniejsze — impulsem dla tego rozumowania jest dążenie do najbardziej racjonalnego wykonania pracy; a więc nie bezmyślnego, mechanicznego powtórzenia rutynowych czynności, ale rozumnego zorganizowania rachunku w sposób najbardziej ekonomiczny. Taką sprawność rachunkową powinna kształcić szkoła, i tylko wówczas będzie prawidłowo przygotowywać swych uczniów do praktycznych zastosowań arytmetyki.

A oto druga sytuacja.

Sposób rozmieszczania towarów na półkach w sklepie samoobsługo-

wym jest zazwyczaj podyktowany tylko zasadą umieszczania obok siebie towarów należących do jednego działu (mydła obok proszków do prania, a nie herbaty). Układ towarów w ramach poszczególnych działów oraz ustawienie poszczególnych półek są w dużej mierze przypadkowe. Klient musi dla zebrania do koszyka potrzebnych mu artykułów przemierzać wnętrze parokrotnie w różnych kierunkach, bądź obejść systematycznie cały labirynt półek, zanim dotrze do kasy. Gdybyśmy przeprowadzili obserwację zakupów, zauważylibyśmy, że niektóre artykuły są kupowane znacznie częściej niż inne. Ustalenie listy tych towarów, na które popyt jest największy, pozwala przeorganizować wnętrze sklepu tak, by znalazła się w nim „linia ekspresowa”, przy której umieszczono by na półkach te właśnie towary (rys. 1). Klient, który chce szybko kupić artykuły pierwszej potrzeby, przejdzie szybko tylko linię ekspresową, nie tracąc niepotrzebnie czasu na błądzenie po sklepie i nie zajmując go innym czekającym na koszyczki.

Rys. 1

Wielu czytelników zapyta zapewne: gdzie tu zastosowanie matematyki? Nie widać, byśmy tu zrobili użytek z algebry, geometrii czy nawet arytmetyki. Rzeczywiście, zastosowania szkolnej wiedzy matematycznej: wzorów, twierdzeń, algorytmów — tutaj nie znajdziemy. Jednak samo podejście do problemu racjonalizacji obsługi klientów ma charakter matematyczny. Na to, by zainicjować opisane badanie, a następnie właściwie wykorzystać jego wyniki, trzeba najpierw stworzyć sobie schemat sklepu-labiryntu, na którym w postaci punktów reprezentowane są towary. Trzeba punktom tym przypisać liczby wskazujące popyt na poszczególne towary. Trzeba wreszcie umieć schemat ten przekształcić tak, by znalazły się na nim możliwie krótkie linie (prowadzące od wejścia do kasy), przy których zgrupowane są punkty przedstawiające towary o największym popycie. Istota tego procesu pozostanie ta sama bez względu na to, czy zostanie on przeprowadzony „w głowie” czy na papierze.

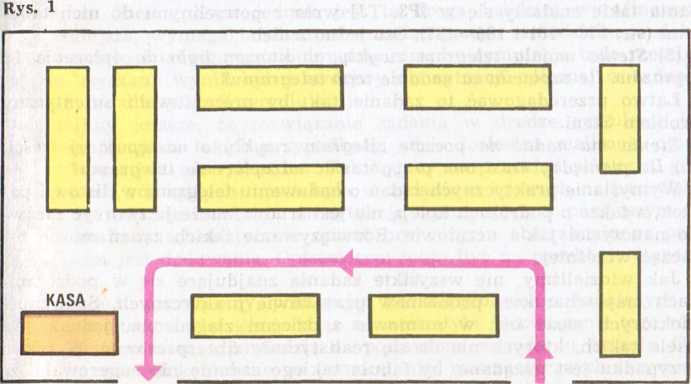
WYJŚCIE    WEJŚCIE