DSC03943

134 WSTĘP DO TECHNIKI ANTENOWEJ

134 WSTĘP DO TECHNIKI ANTENOWEJ

Wstawiając (7.15) do (7.12) i porównując poszczególne składowe otrzymujemy

następujący układ równali:

V²A_x+p²A_x = — li    f. ^7.16a)

^Ay + ^Ay i -Jy    .

^A,+p²A_z i -J_z    (7.16c)

gdzie fi² = orfie. Założymy w tym momencie, że fala rozchodzi się w próżni, więc cr = 0 i współczynnik fazy jest liczbą rzeczywistą:

p = (o-y/iie    (7.17)

Wszystkie trzy równania (7.16) mają identyczną postad, wystarczy więc znaleźć rozwiązanie dla jednego z nich. Na początku znajdziemy rozwiązanie dla źródła punktowego, które może być przybliżone za pomocą dystrybucji Diraca:

V²\j/+P²\j/ ||-5(x)8(y)6(z)    ^7.18|_:

gdzie \J/ jest odpowiedzią na źródło punktowe umieszczone w początku układu współrzędnych. Jeśli prąd płynie w kierunku z, to \|/ = A_z. Dla wszystkich punktów oprócz początku układu współrzędnych słuszne jest równanie

V²\j/+p²\jf=;0    (7.19)

zwane skalarnym równaniem falowym lub równaniem Helmholtza. Z powodu symetrii laplasjan zapisujemy we współrzędnych sferycznych i wtedy \|/ zależy tylko od odległości od środka układu. Dwa rozwiązania (7.19) są postaci e^-Jpr/r oraz e^/r. Odpowiadają one odpowiednio falom rozchodzącym się od środka układu i do środka układu współrzędnych. Fizyczne znaczenie ma tylko rozwiązanie dla fali poruszającej się na zewnątrz, co daje nam następujące rozwiązanie dla źródła punktowego (po oszacowaniu współczynnika proporcjonalności):

(7.20)

Jest to tzw. funkcja Greena, która określa odpowiedź w odległości r od punktowego źródła umieszczonego w początku układu współrzędnych. Jeśli źródło leży poza początkiem układu, to musimy obliczyć odległość R pomiędzy położeniem źródła a punktem obserwacji P (rys. 7.5). Wtedy rozwiązanie (7.20) wygląda następująco:

11='

_e-JP^R

4nR

(7.21)

Dla dowolnego rozkładu prądu płynącego wzdłuż osi z potencjał wektorowy ma tylko składową z-ową. Jeżeli przyjmiemy, że źródło jest zbiorem źródeł punktowych o amplitudzie prądu ważonej przez rozkład J_z, to odpowiedź A_z jest ważoną sumą odpowiedzi na źródła punktowe (7.21). Można ją wyrazić jako całkę po objętości v':

z

A

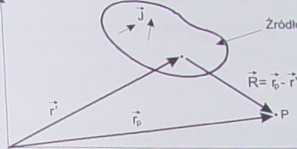
Źródło o objętości V

+-y

x

Rys. 7.5. Geometria systemu ze źródłami promieniowania

J,

_e-JPR

^z 4kR

dv'

(7.22)

Podobne równania obowiązują dla składowej x i y. Całkowite rozwiązanie jest sumą po wszystkich składowych:

_e-iP^R

A =    J—— dv'

jjg 4tcR

(7.23)

Wzór (7.23) jest rozwiązaniem wektorowego równania falowego (7.12). Geometria systemu, dla którego ułożono równanie, jest przedstawiona na rys. 7.5. Wektor r' łączy środek układu z dowolnym punktem wewnątrz źródła, r_p jest wektorem między środkiem układu a punktem obserwacji P, natomiast R łączy źródło z punktem obserwacji i jest równy r_p— r'.

Podsumujmy procedurę znajdowania pól wytwarzanych przez źródło o rozkładzie objętościowym prądu J. W pierwszym kroku znajdujemy A z równania (7.23). Pole magnetyczne H otrzymujemy z (7.4). Pole elektryczne można obliczyć z (7.13), częściej jednak wykorzystuje się przekształcone równanie (7.2):

^— jme,

jeśli znajdujemy się w obszarze zajmowanym przez źródło lub

(7.24)

(7.25)

E = -—V x H j(OE ■

7.3. Dipol idealny

Zajmiemy się teraz analizą dwóch ładunków znajdujących się bardzo blisko siebie (Az -> 0 lub Az « X) i połączonych nieskończenie cienkim przewodem. Rozkład prądu płynącego wzdłuż przewodu jest równomierny, a sam element jest umiesz-