DSC03952

ISO WSTĘP DO TECHNIKI ANTENOWEJ

otrzymujemy

n

(Zp — impedancja falowa próżni)

oraz

(7.79)

(7.80a)

(7.80b)

Podstawiając podane wzory do (7.78) dostajemy

(7.81)

gdzie d£2 = sin0d0d<t> jest różniczką kąta bryłowego (patrz dodatek). Całkowanie można przeprowadzić po dowolnej powierzchni obejmującej antenę, jednak ze względu na prostotę zwykle całkuje się po powierzchni kuli o środku umieszczonym w początku układu współrzędnych. Ponieważ amplitudy pól są funkcją 1/r, dogodnie jest wprowadzić parametr zwany gęstością promieniowania (nie mylić z powierzchniową gęstością mocy), który jest zdefiniowany następującym równaniem:

(7.82)

Gęstość promieniowania jest mocą wysyłaną w danym kierunku w jednostce kąta bryłowego (steradian) i jest podawana w W/sr. Nie zależy ponadto od odległości r. Można ją wyrazić za pomocą unormowanej charakterystyki promieniowania: -K

U(0,<j>) = UJF(0, <j))|²

(7.83)

gdzie U_m jest maksymalną gęstością promieniowania

U_ra = U(0max , $max)

(7.84)

Całkowita moc promieniowana przez antenę jest otrzymywana poprzez sumowanie (całkowanie) gęstości promieniowania we wszystkich kierunkach (po wszystkich kątach wokół anteny):

Ppr = H U(0, $) dQ = U_m JJ |F(0, <|>) I² dQ

(7.85)

Przy definiowaniu kierunkowości i zysku energetycznego użyteczne jest pojęcie anteny izotropowej. Jest to antena, która wysyła energię jednakowo we wszystkich kierunkach Ponieważ każde rzeczywiste źródło promieniowania jest rozciągłe w przestrzeni, zatem antena izotropowa nie jest realizowalna fizycznie. Charakterystyka promieniowania anteny izotropowej ma postać powierzchni kuli. Gęstość promieniowania we wszystkich kierunkach jest jednakowa i wynosi U_nve. Moc promieniowana przez antenę izotropową wynosi P_pr = JJ U,_vcdT2 =

= U_uvc JJ dQ = 4nU_ave. Dla anten innych niż izotropowa gęstość promieniowania zależy od kierunku, ale możemy zdefiniować średnią gęstość promieniowania jako

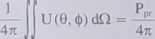
(7.86)

Średnia gęstość promieniowania może być interpretowana jako gęstość promieniowania anteny izotropowej promieniującej taką samą moc jak rozważana antena rzeczywista. Jako przykład rozpatrzmy dipol idealny. Gęstość promieniowania jest w tym przypadku równa (wzory 7.37,7.38 i 7.82)

F(9,<|») = sin0

(7.87)

gdzie:

(7.88)

(7.89)

Średnia gęstość promieniowania dla dipola idealnego wynosi

P_pr (Pcoh/12tc)(IAz)² 1 /IAz\. 2,    .

Wynik U_m = l,5U_ave oznacza, że w kierunku maksymalnego promieniowania gęstość promieniowania jest o 50% większa niż ta, która wystąpiłaby w przypadku anteny izotropowej promieniującej taką samą moc jak dipol idealny.

Zdefiniujmy teraz zysk kierunkowy (lub funkcję kierunkowości) jako stosunek gęstości promieniowania w danym kierunku do uśrednionej gęstości promieniowania:

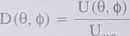
uve

(7.91)

Jeśli podzielimy licznik i mianownik przez r², to otrzymamy gęstości powierzchniowe mocy. Zysk kierunkowy jest więc stosunkiem powierzchniowej gęstości mocy w pewnym kierunku w ustalonej odległości r do uśrednionej powierzchniowej gęstości mocy w tej odległości:

— 2    U(0,(j>)/r²    l/2ReQ§ x H*) • f

D(v|    -

(7.92)

Podstawiając (7.86) do (7.91) mamy

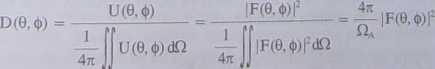
(7.93)