DSC03955

156 WSTĘP DO TECHNIKI ANTENOWE!

O

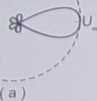
Rys. 7.17. Ilustracja EIRP; a) antena kierunkowa o mocy P« i zysku G, . b) antena izotropowa zasilana mocą P_WCG i jednostkowym zysku (w obu przypadkach zastępcza moc

(b)

promieniowana izotropowo jesi identyczna)

Jeśli badana antena na danym kierunku ma zysk G, to natężenie pola w punkcie odbioru, pochodzące od tej anteny zasilanej mocą P_we, byłoby równe natężeniu wytwarzanemu przez bezstratną antenę izotropową o zysku G = 1 zasilaną mocą PweG (rys. 7.17). Zastępcza moc promieniowana izotropowo jest wykorzystywana przy obliczeniach propagacyjnych.

7.4.4. Impedancja wejściowa

Impedancja wejściowa anteny jest definiowana jako impedancja widziana na zaciskach anteny. Jest ona równa stosunkowi napięcia na zaciskach anteny do wpływającego prądu. Musimy zatem zawsze określać położenie zacisków w antenie. Na impedancję wpływa obecność innych anten lub obiektów znajdujących się w pobliżu. Dokładniej omówimy te zagadnienia przy okazji wyjaśniania pojęcia impedancji wzajemnej.

Impedancja wejściowa anteny składa się z części rzeczywistej i urojonej:

(7.111)

Z_we — R_we+jX_we

Rezystancja wejściowa R_we reprezentuje straty energii, która może być rozpraszana dwojako. Część mocy jest zużywana na ogrzanie elementów anteny (straty cieplne). Reszta energii jest rozpraszana w wyniku wypromieniowania jej przez antenę w otaczającą przestrzeń (strata „pożądana”). Średnia, całkowita moc rozpraszana w antenie wynosi

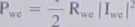
(7.112)

gdzie I_we jest prądem na zaciskach anteny (amplituda). Rozdzielając moc wejściową na straty cieplne i promieniowanie mamy

(7.113)

P- - Ppr + Ps,r = y Rpri|Iwe|²fyR»«r|Iwe|²

gdzie definiujemy rezystancję promieniowania anteny odniesioną do zacisków wejściowych jako

(7.114)

a rezystancję strat jako

(7.115)

Wypromieniowana przez antenę moc jest równa

2P_s«r _ 2(P_we-P_pr)

^Ks(r — ,_T j₂    |T |2

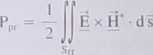
(7.116)

gdzie Sfr jest powierzchnią (najczęściej kuli) w strefie promieniowania. Zespolony wektor Poyntinga jest rzeczywisty w strefie promieniowania. Rezystancja promieniowania może być zdefiniowana względem prądu płynącego w dowolnym miejscu anteny. Zwykle używamy maksymalnej wartości prądu w antenie i tak określoną rezystancję będziemy oznaczać jako R_pr. R_pri oznacza rezystancję promieniowania widzianą na zaciskach. Ponieważ w tym podrozdziale będziemy zajmować się elektrycznie krótkimi antenami, dla których prąd osiąga maksimum właśnie na zaciskach i zachodzi Rpn = Rpr, będziemy oznaczać rezystancję promieniowania jako R_pr.

Jako przykład rozważmy dipol idealny, dla którego moc promieniowana jest dana wzorem (7.40). Rezystancja promieniowania jest w tym przypadku równa

i ostatecznie

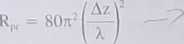
(7.118)

Ponieważ rozmiar dipola idealnego jest znacznie mniejszy niż długość fali, R_pr jest bardzo mała.

Sprawność energetyczna anteny może być wyrażona za pomocą zdefiniowanych rezystancji:

Pnr. ₌ Pp, ₌ 0.5R_prilIwcl²

*1 D    D i D    A <D IT |2 i (KD

Pwe Ppr+P* . 0,5R_pri|I_wep + 0,5RJIJ²

^ Rpri + Rsir Rwi

(7.119)

Dla wielu anten sprawność energetyczna jest bliska 100%. Dla anten elektrycznie krótkich sprawność jest bardzo mała. Na przykład dla dipola idealnego o długości Az = 1 m = 0,0033A. rezystancja promieniowania wynosi 0,0088 Q dla częstotliwości 1 MHz. Rezystancja strat w antenie ze stałym rozkładem prądu o długości Az wynosi [9]

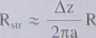
(7.120)

gdzie R_s jest rezystancją powierzchniową (wzór 2.61), natomiast a oznacza promień drutu, z którego wykonano antenę. Jeśli nasz dipol wykonamy z miedzi,