DSC03946

138 WSTĘP DO TECHNIKI ANTENOWEJ

magnetyczne ma składową H*. Pola w strefie indukcji są bardzo skomplikowane. Pole elektryczne jest przesunięte w fazie względem pola magnetycznego o 90° (pomijamy „1” w 7.36), dlatego też licząc wektor Poyntinga otrzymamy wartość 0. Oznacza to, że dipol w strefie bliskiej nie promieniuje energii na zewnątrz. Jest ona magazynowana w polu elektrycznym i magnetycznym, podobnie jak energia magazynowana w cewce lub kondensatorze.

W miarę wzrostu odległości punktu obserwacji od dipola maleje wkład pochodzący od składników z r w mianowniku. Składowe pola elektrycznego stają się przesunięte w fazie o 90° i wypadkowy wektor E jest spolaryzowany eliptycznie. Składowe Eq i H₀ stają się współfazowe, dlatego wektor Poyntinga przyjmuje wartości niezerowe (oznacza to przepływ energii wzdłuż kierunku propagacji — pojawia się promieniowanie). Strefa, w której zachodzą powyższe zjawiska, dla której pr > 1, nosi nazwę strefy pośredniej (Fresnela). Pola w tej strefie są również dość skomplikowane, a zależności (7.35) i (7.36) można uprościć poprzez pominięcie składników z r w mianowniku.

Dla bardzo dużych odległości od dipola (r » A.) pomijamy w nawiasach wszystkie składniki z r. Dodatkowo zauważmy, że składowa Er maleje odwrotnie proporcjonalnie do r², dlatego dla dużych r możemy ją pominąć. Ostatecznie

pozostaną tylko składowe Ee i H*:
P IAz S e“^jPr SI E = ——jou-sin 00 i\|\|g\| 4it r	(7.37)
m iaz. iii H = ——jP-sin 0$ i	(7.38)
Strefę tę nazywamy strefą promieniowania (daleką lub Fraunhofera). Pole elektryczne jest w niej prostopadłe do pola magnetycznego i w danym punkcie prostopadłe do kierunku rozchodzenia się fali. Fala pochodząca od dipola jest falą sferyczną, jednak w strefie dalekiej na małym obszarze (tym większym, im dalej od źródła) ma ona lokalnie charakter fali płaskiej typu TEM. W powietrzu lub wolnej przestrzeni stosunek obu składowych wynosi
iSSB»	{(7.39)

a więc jest równy impedancji falowej próżni. Obliczmy jeszcze zespoloną moc przepływającą przez powierzchnię kuli o dostatecznie dużym promieniu r ze środkiem położonym w centrum dipola:

Ppr = -yjl*H--dS

2x x

l /IAz\²

nilli

,-jPf

,+jPr

-sin 00 x (— jB)-sin 0<fr • ds =

i mm

1 /IAz\² _ f f sin²0 ,

(7.40)

= g>pP 1 I—?• Psinedtyder =

^fi"‘^p24⁼^-^ciĄz)l

⁼ ł(^r) ■- i©

Wektor Poyntinga w strefie promieniowania jest rzeczywisty. oznacza moc wypromieniowaną przez dipol w przestrzeń. Moc ta nie zalety od promienia r.

Z mocą promieniowaną przez antenę ma związek jej impedancja wejściowa, którą omówimy później. Opisane własności pól wytwarzanych przez dipol idealny odnoszą się do wszystkich źródeł promieniowania.

Ponieważ większość parametrów anten jest definiowana i mierzona w strefie promieniowania, dlatego też niezwykle ważne staje się określenie kryteriów odległościowych podziału na strefy. Aby to uczynić, rozważymy prosty przykład anteny liniowej o skończonej długości, umieszczonej w początku układu współrzędnych wzdłuż osi z (rys. 7.7). Wiele anten stosowanych w praktyce może być przybliżonych przez to źródło liniowe (np. dipol półfalowy). W tym przypadku potencjał wektorowy ma tylko składową z, a całka potrójna redukuje się do całki liniowej po z:

A_z

I(z')

_e-jPR

4tiR

dz'

(7.41)

Z powodu symetrii źródła pola przez nie wytwarzane nie będą się zmieniać w funkcji kąta <|>. Kiedy obserwator zaczyna okrążać źródło w takiej samej odległości r i dla stałej współrzędnej z, widok anteny pozostaje nie zmieniony; podobnie dzieje się też z polami. Dla ułatwienia wybierzemy sobie punkt obserwacji w płaszczyźnie yz (<{> = 90°). Zachodzą następujące zależności (patrz rys. 7.7)^

ssSIS i . 81

jr+z |

(7.42)

ż = ir cós0

(7.43)

y = rsinO

(7.44)

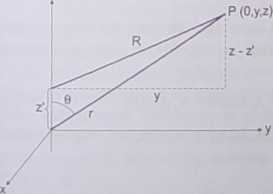
Rys. 7.7. Geometria do obliczeń źródła liniowego