DSC03961

168 WSTĘP DO TECHNIKI ANTENOWEJ

Obszar v_a

Obszar v_b

Rys. 7.26. Konfiguracja źródeł do twierdzenia o wzajemności

rodzaju urządzenia iskrzące i przełączające (przełączniki, spawarki, układy zapłonowe aut, falowniki tyrystorowe, układy odchylające TV) oraz urządzenia wytwarzające celowo energię elektromagnetyczną (nadajniki, zgrzewarki, diatermie krótkofalowe i mikrofalowe itp.).

Na wypadkową zastępczą temperaturę szumów anteny składają się szumy pochodzące z obiektów zewnętrznych oraz szum termiczny samej anteny (rezystancja strat). Zastępcza temperatura szumów zewnętrznych zależy od charakterystyki promieniowania anteny i temperatury zastępczej źródeł szumu:

o o

(7.153)

gdzie T_A jest zastępczą temperaturą źródeł zewnętrznych, T_s(0, <|>) jest rozkładem temperatury źródła w funkcji kątów, f2_A jest zastępczym kątem pełnej mocy anteny, natomiast G(0, <J>) jest funkcją zysku energetycznego zdefiniowaną wzorem (7.102). Całkowita temperatura zastępcza anteny wynosi [6]

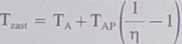
(7.154)

gdzie Tąp jest fizyczną temperaturą anteny, a r\ jej sprawnością energetyczną Dokładną analizę szumów (połączenie antena — odbiornik) można znaleźć w [6].

W literaturze spotyka się czasem pojęcie współczynnika przydatności stacji odbiorczej G/T. Jest to stosunek zysku energetycznego anteny do zastępczej temperatury szumów będącej wypadkową temperatury szumowej anteny, linii transmisyjnej i odbiornika. Jednostką współczynnika przydatności jest dB/K.

7.5. Zasada wzajemności

w których płyną prądy (rys. 7.26). Niech źródła J. i M„ wytwarzają odpowiednio

Omówimy teraz bardzo ważne twierdzenie w teorii anten zwane zasadą wzajemności W tym celu wyjdziemy od zasady wzajemności zdefiniowanej przez Lorentza dla dowolnych pól elektromagnetycznych. Załóżmy, że dane są dwa obszary,

pola E_a i H_a, natomiast źródła Jj, i Mb pola Et, i H*,. Niech częstotliwości w obu przypadkach będą takie same. Dla ośrodków izotropowych zachodzi wtedy równość [9]

(7.155)

^ ^Vb

Lewa strona równania jest miarą sprzężenia pól wytwarzanych przez źródło b na źródło a, natomiast prawa strona opisuje sprzężenie pól wytwarzanych przez źródło a ze źródłem b. Załóżmy teraz, że źródło b jest dipolem idealnym o długości wektorowej p, który jest umieszczony w punkcie (Xp, y_p, z_p). Ponieważ w dipolu M_b = 0, a prąd możemy zapisać jako

x_p) 8(y—y_p)8(z—Zp)p    (7.156)

to równanie (7.155) przekształca się do

ia(Xp> y_P, Z_p) • p = UJ (E_b • Ł-Hb • M,) d/    (7.157)

v, •

Podane wyrażenie pozwala nam obliczyć pole elektryczne ze źródeł a poprzez obliczenie całki z wykorzystaniem znanych źródeł J, i M, i znanych pól pochodzących od dipola Eb i H_b (wzory 7.33 i 7.34). Zasada wzajemności Lorenza może być użyta do wyprowadzenia zasady wzajemności dla anten wykorzystującej napięcia i prądy na zaciskach anten. Załóżmy, że źródła a i b są antenami pobudzanymi przez idealne źródła prądowe L, oraz I_b. Ponieważ nie ma źródeł prądu magnetycznego, więc (7.155) przyjmuje postać

Jlflfł.dY' = JIJE.-L.dv' ^! ■    ' I (7.158)

V_a    V_b

Dla doskonale przewodzących anten pole elektryczne będzie równe zeru na ich powierzchni, ale na zaciskach pojawi się niezerowe napięcie, które można obliczyć ze wzoru (1.17). Wzór (7.158) przekształca się do postaci

. ItfJuFIb    1 ||j| _x.(7:i59)

gdzie U“ jest napięciem na otwartych zaciskach anteny a wytworzonym przez pole Eb generowane przez antenę b, a U_b^c jest napięciem na otwartych zaciskach anteny b wytworzonym przez antenę a. Równanie (7.159) możemy zapisać w postaci proporcji:

(7.160)

U” UF Ib I T V

Na napięcie indukowane na otwartych zaciskach anteny wpływają takie czynniki jak typ anteny, ośrodek między antenami oraz przedmioty znajdujące się w ich pobliżu. Ogólnie możemy przedstawić tę sytuację korzystając z parametrów obwodowych:

(7.161a)

UaH Zaola + Zablb