DSC03947

140 WSTĘP DO TECHNIKI ANTENOWEJ

Widzimy też, źe r_p = r = yy + zż i T = z'ż, co prowadzi do R = r_p—r' = y$ + +(z—z02 i dalej

R = y/f+(z-z')² =    y²+ z²—2zz?+ (zT)²    (7.45)

Podstawiając (7.42) i (7.43) do (7.45) w celu wyrażenia wszystkich współrzędnych w układzie sferycznym mamy

R = ^/r²+[ ~ 2r cos Qzf(z⁷)²]    (7.46)

Aby otrzymać przybliżone wyrażenie na R, rozwiniemy (7.46) za pomocą dwumianu:

_n , _n (zO² (zO²cos²0

R = r—z cos0H—-—-----4- ... =

(7.47)

j : 2t . . 2r

i | (zO²sin²0

= r— z cosO-fr. - -.-+ ...

B | ■ j    2r

Składniki w podanym szeregu maleją wraz ze wzrostem potęgi z', jeśli z'jest małe w porównaniu z r. Otrzymane wyrażenie na R jest używane w całce (7.41) w różnym stopniu przybliżenia. W mianowniku (wpływającym tylko na amplitudę) wstawiamy

|R| = Rsr    (7.48)

Możemy tak uczynić, gdyż w strefie promieniowania r jest bardzo duże w porównaniu z rozmiarem anteny (r»z' ^ z'cos0). W wykładniku — |3R musimy zachować większą dokładność. Całka (7.41) sumuje wkłady pochodzące ze wszystkich punktów leżących wzdłuż źródła punktowego. Chociaż amplitudy fal pochodzących z każdego punktu są zasadniczo takie same, fazy mogą być różne, jeśli różnice dróg są porównywalne z długością fali. Użyjemy zatem dwóch pierwszych składników rozwinięcia (7.47) w liczniku

R 8 r—1| cos0    (7.49)

Ostatecznie całka przybierze postać

f    g-jPrfr-^cwG)    _e—jpr f

A_z = I (zO-gS-dz'= —— I(z') e^⁰⁵⁹ dz'    (7.50)

J    4nr    4nr J

Całkujemy oczywiście tylko wzdłuż źródła liniowego. Możemy dostrzec wyraźne podobieństwo (7.50) do całek występujących w zespolonym szeregu Fouriera. Obliczamy następnie pole magnetyczne:

H = V x A = V x (A₇ż) = V x (—A_z sin 00 + A_z cos0r)    (7.51)

Ponieważ zapisaliśmy A₇ jako funkcję r i 0, liczymy rotację we współrzędnych sferycznych i dostajemy

H =

d ,    _ d

— (-rA* sin 0)- — (A_z cos 0)

(7.52)

Podstawiając (7.50) mamy dalej

H = $ (    f--- I (z') e⁵^”*⁰ dz'—e^-jPr—

l 4nr [■    ^    ■

:gŚ^i|- ,^l    _r_    ||l

-4^00 [^COS0f^I(^^C“°dz']j =

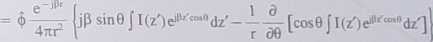
(7.53)

Stosunek pierwszego do drugiego składnika w nawiasie jest rzędu pr. Jeśli Pr » 1, to drugi składnik jest znacznie mniejszy w porównaniu z pierwszym i można go pominąć. Ostatecznie pole magnetyczne w strefie promieniowania, pochodzące od źródła liniowego, jest równe

(7.54)

i§ ■    ;. • :erlMP»l

H = $jpsin0-^- I(z^/)e^jpz'^cos0dz^/ = $jpsin0A*

Pole elektryczne można znaleźć ze wzoru (7.13). Podstawiając do tego wzoru (7.41) i uwzględniając tylko składniki znaczące w strefie promieniowania, otrzymujemy przybliżenie dla tej strefy:

(7.55)

E = — j©pA_o0 = Ojcop sin 0 ^

Zatem w strefie dalekiej źródło liniowe wytwarza składowe i Ę,. Jedynym problemem pozostaje obliczenie A_z i jest to kluczowy punkt w analizie anten.

Stosunek E₀ do jest równy impedancji charakterystycznej ośrodka Składowe pól są wzajemnie do siebie prostopadłe i jednocześnie prostopadłe do kierunku propagacji. Są to cechy fali płaskiej, przy czym tutaj faza na płaszczyźnie ulega zmianie, a amplituda jest proporcjonalna do 1/r. Powiedzieliśmy już sobie, że jest to fala lokalnie płaska. Dzięki temu znając jedną składową pola możemy z prostych zależności dla fali płaskiej obliczyć drugą składową. Odnosi się to do wszystkich źródeł promieniujących, jeśli tylko znajdujemy się w strefie promieniowania. Zakładając ponadto, że fala wytwarzana przez źródło jest kulista, amplituda pola elektrycznego i magnetycznego w tej strefie jest proporcjonalna do 1/r.

Przedstawione przybliżenia dla strefy promieniowania mają prostą interpretację geometryczną. Jeśli narysujemy promienie z każdego punktu źródła jako linie równoległe (rys. 7.8), możemy łatwo zweryfikować prawidłowość przybliżenia (7.49). Promienie będą dokładnie równoległe tylko wtedy, gdy punkt obserwacji P będzie znajdował się w nieskończoności, ale dla strefy promieniowania jest to dobre przybliżenie. Obliczenia w wielu przypadkach rozpoczyna się od przyjęcia założenia o równoległości promieni, a następnie liczy się R z zależności geometrycznych. Rozważmy dowolne źródło przedstawione na rys. 7.9. Wynika z niego, że

(7.56)

R = r—/cos a