DSC03945

136 WSTĘP DO TECHNIKI ANTENOWEJ

z

x

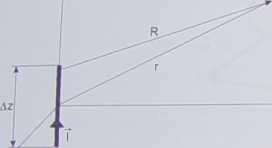
Rys. 7.6. Dipol idealny z równomiernym rozkładem prądu

-•P

►y

czony wzdłuż osi z w początku układu współrzędnych (rys. 7.6). Taką strukturę zwiemy dipolem idealnym. Nie występuje on samodzielnie, ale może być bardzo małym fragmentem prądu płynącego w antenie rzeczywistej. Fizyczny model dipola idealnego powstały poprzez dołączenie pojemności wierzchołkowych (których działanie omówimy nieco później) nosi czasem nazwę dipola Hertza. Analiza pól dipola idealnego jest ważna z praktycznego punktu widzenia, gdyż niektóre wnioski odnoszą się do wszystkich źródeł promieniowania. Pola wytwarzane przez dipol przybliżają pola wytwarzane przez elektrycznie małe anteny analizowane w rozdziale 8.

Dla elementu o równomiernym rozkładzie prądu wzdłuż osi z o amplitudzie I wzór (7.23) na potencjał wektorowy redukuje się do całki pojedynczej po z:,

A = żl

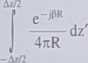
(7.26)

Az jest bardzo małe w porównaniu z długością fali oraz R i dlatego odległość R między punktami umieszczonymi na dipolu a punktem obserwacji jest w przybliżeniu równa odległości r między początkiem układu a punktem obserwacji P. Podstawiając r za R w (7.26) i całkując otrzymujemy

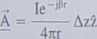
(7.27)

Dla wielu źródeł z prądem możemy dokonać zamiany R na r w mianowniku (7.26), ale zwykle nie możemy tego uczynić w wykładniku. Jest to możliwe tylko w przypadku bardzo małych źródeł.

Obliczymy teraz pola wytwarzane przez dipol idealny. Pole magnetyczne jest równe

(7.28)

H = V x A = V x (A₁ż)

Stosując tożsamość wektorową (dodatek C.9) otrzymujemy

H = (VA_Z) x ż + A_Z(V x z) = (VA*) x ż

(7.29)

Drugi składnik w powyższym wzorze jest równy 0 (rotacja ze stałej). Podstawiając (7.27) do (7.29) dostajemy

(7.30)

Obliczając gradient we współrzędnych sferycznych mamy

Wykorzystując zapis wersora ż we współrzędnych sferycznych w iloczynie

r x ż = f x (r cos0 — OsinO) = — $sin0 wstawiamy go do (7.31):

(7.31)

(7.32)

ij ₌ J£L[JE ₊ JL]_e-HM

4tc l r r* J '

JAz

47C

(7.33)

Pole elektryczne wytwarzane przez dipol idealny możemy obliczyć z równania (7.25). Wynosi ono

Lr y e r² j<

Je~^jPrsin 00 +

jcoer

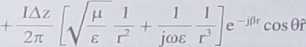
(7.34)

Pominęliśmy dla uproszczenia w zapisie zależność od czasu (zapis pełny d^(u* ^pr)...). Równania (7.33) i (7.34) możemy przepisać w bardziej dogodnej do analizy postaci:

(7.35)

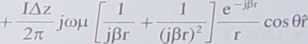
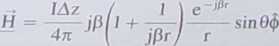
(7.36)

Pole elektryczne wytwarzane przez dipol idealny ma w ogólności dwie składowe: E_r i Eq, natomiast pole magnetyczne ma składową H$.

Struktura pola elektromagnetycznego wokół dipola zmienia się w zależności od odległości obserwacji. Jeśli znajdujemy się bardzo blisko dipola (r « X lub fir«A), to składniki w nawiasach wzorów (7.35) i (7.36) przyjmują znaczące wartości (możemy nawet pominąć „1” w nawiasach). Mówimy wtedy, że znajdujemy się w strefie indukcji (strefie bliskiej). Pole elektryczne ma dwie składowe: E_r i E₀ (są one współfazowe względem siebie), natomiast pole