DSC03948

142 WSTĘP DO TECHNIKI ANTENOWEJ

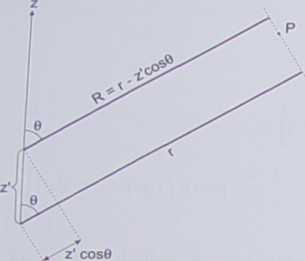
Rys. 7.8. Przybliżenie promieniami równoległymi dla źródła liniowego

Wykorzystując definicję iloczynu skalarnego możemy zapisać ten wzór następująco:

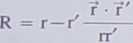
(7.57)

lub

(7.58)

R = r—f • r'

Zwróćmy uwagę, że gdy r' = z'ź (jak mamy w przypadku naszego źródła liniowego), wzór (7.58) upraszcza się do (7.49). Równanie (7.58) opisuje R w strefie promieniowania w celu użycia tego przybliżenia w wykładniku określającym fazę.

Definicja odległości, dla której zaczyna się strefa promieniowania, jest oparta na określeniu odległości r, dla której przestaje obowiązywać przybliżenie mówiące o równoległości promieni. Mówiąc dokładniej, odległość r_ff, w której zaczyna się strefa promieniowania, jest tą wartością r, dla której zmiana długości wynikająca z pominięcia trzeciego składnika rozwinięcia (7.47) wynosi jedną szesnastą długości fali. Odpowiada to błędowi fazy równemu 2nTk • A/16 =

= -£-rad | 22,5°.

o

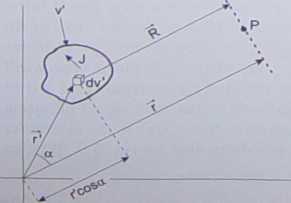
Rys. 7.9. Przybliżenie promieniami równoległymi dla źródła o dowolnych rozmiarach

Jeśli D jest długością źródła liniowego, odległość r_ff jest znajdowana poprzez przyrównanie maksymalnej wartości trzeciego składnika rozwinięcia (7.47) (z' = D/2 i 0 = 90°) do 7J16:

(7.59)

(7.60)

(D/2)² X 2r_n Wrn

Rozwiązując to równanie dostajemy 2D² '

ESH

W przypadku dowolnej anteny D jest jej największym rozmiarem liniowym (długość dipola, średnica anteny parabolicznej itp.). Możemy teraz określić warunki wyznaczające pole dalekie anteny:

	(7.61)
r » D	(7.62)
r » X	(7.63)

Warunek (7.62) wynika z przybliżenia we wzorze (7.48) dla potrzeb określenia amplitudy pola. Warunek (7.63) wynika z kolei z warunku Pr = (2mIX)»1 wykorzystanego przy redukcji wzoru (7.53) do (7.54). Należy zauważyć, że strefa daleka zaczyna się w momencie, gdy spełnione są jednocześnie wszystkie trzy warunki. W zakresie fal UKF wystarcza zwykle warunek (7.61), dla fal o mniejszych częstotliwościach, gdy rozmiary anten są często małe w porównaniu z X, początek strefy wyznaczają dwa pozostałe warunki.

Warunki dla określenia granicy strefy pośredniej i indukcji wynikają z dokładniejszego przybliżenia r wzorem (7.47). Uwzględniamy teraz trzy pierwsze wyrazy rozwinięcia. Błąd będzie zatem brał się głównie z pominięcia czwartego wyrazu. Aby określić maksymalny błąd fazy, musimy najpierw wyznaczyć kąt 0, dla którego czwarty wyraz osiąga maksimum. W tym celu różniczkujemy go i przyrównujemy pochodną do zera:

d_

30

' 1 MO³

—r- I-cos 0 sin 0

niSg ... h

(z')³

= —j-sin0[—sin²0+2cos²0] = 0

(7.64)

Odrzucamy jako rozwiązanie 0 = 0, gdyż cały wyraz przybiera zerową wartość (najmniejszy błąd). Największy błąd występuje wtedy, gdy znika drugi składnik (7.64), czyli

[—sin²0 + 2cos²0]|e.0, = O=^0| = arctg(±-«/2):.,‘..    (7.65)

Jeśli przyjmiemy, że maksymalny błąd fazy nie może przekraczać rc/8, to odległość r, dla której to następuje, może być znaleziona z równania