HWScan00197

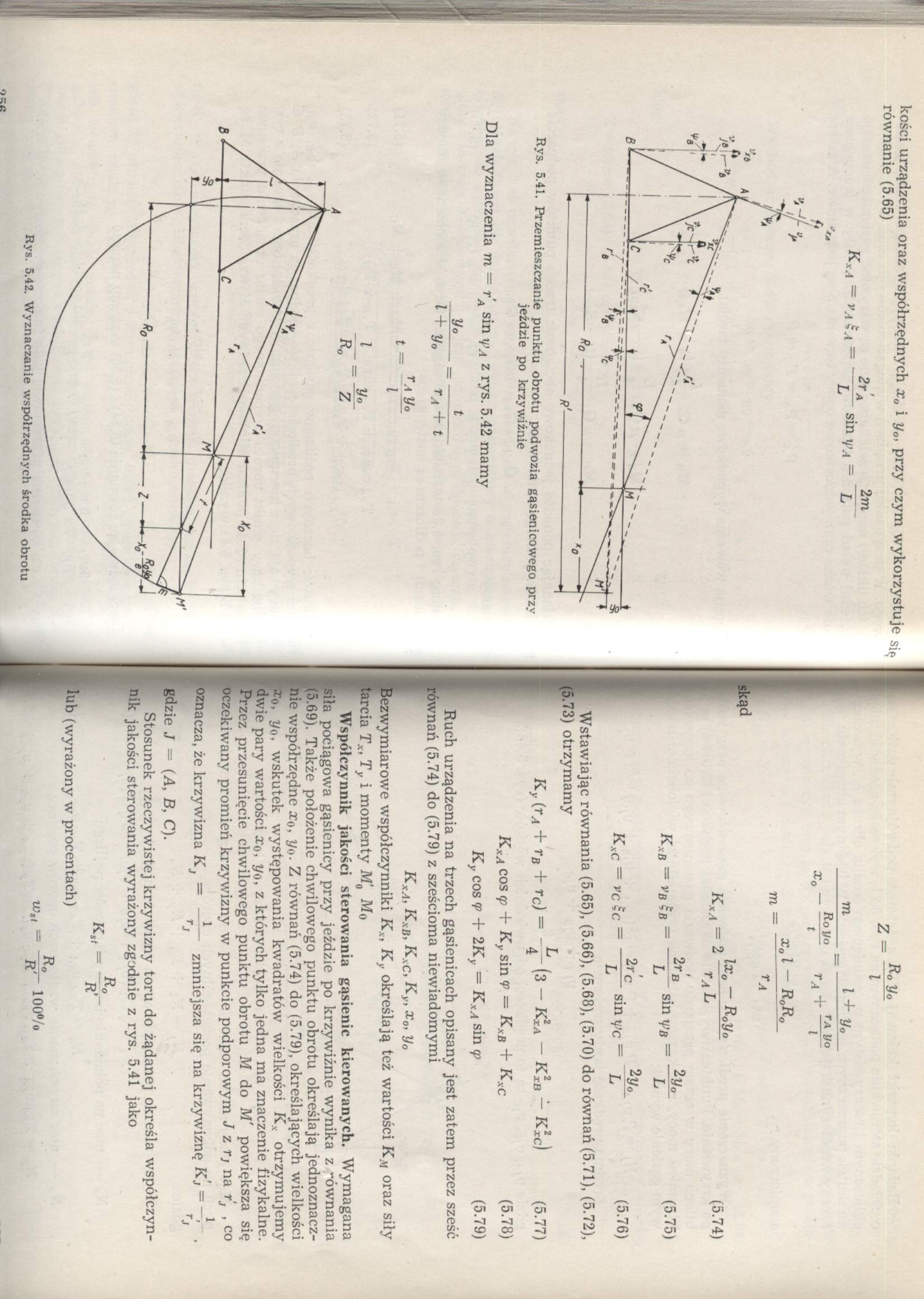
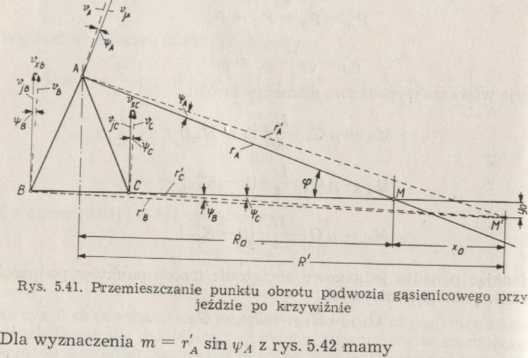
°^{raz współrzędnych} x° ¹ y°’ P^rzy ^czy^m wykorzystuje

równanie (D.oDj

2r j

^K.x_A = V_A =

_L sm = L

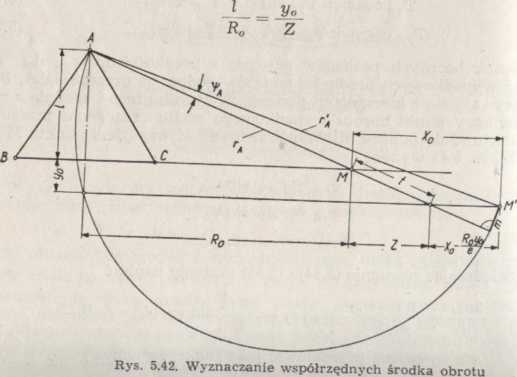
i+2/₀

r_A + t

2 m

, _ r_Ayo ¹ l

cza

₌ Rcy_t l

m_

_ Royo

l + Vo

, ta Ho

r A + ——

x_Q l RqRq

~ r_A

z*. - Ky„ ^k*a ~ * rA L		(5.74)
2t k,b = v„ h = —fT^sinVB =	2 y0 L	(5.75)
2 .	tyo	(5.76)
KxC = vc£c- L ^sin Wc -	L

skąd

Wstawiając równania (5.65), (5.66), (5.68), (5.70) do równań (5.71), (5.72), (5.73) otrzymamy

K_y (t_a + Tb + r_c) =    (3 “ Rxa ~ K²xb ~ Kxc) (5.77)

K_xA cos (p + K_y sin V = K_xB + K_xC    (5.78)

K_y cos V + 2K_y = K_xA sin cp    (5.79)

Ruch urządzenia na trzech gąsienicach opisany jest zatem przez sześć równań (5.74) do (5.79) z sześcioma niewiadomymi

K-x_Ai K_xB, R-xCt K_y, x₀, y₀

Bezwymiarowe współczynniki K._v, K_y określają też wartości K_M oraz siły tarcia T_x, T_y i momenty M'₀ Mo

Współczynnik jakości sterowania gąsienic kierowanych. Wymagana siła pociągowa gąsienicy przy jeździe po krzywiźnie wynika z ~ównania (5.69). Także położenie chwilowego punktu obrotu określają jednoznacznie współrzędne x₀, y₀. Z równań (5.74) do (5.79), określających wielkości x₀, y₀, wskutek występowania kwadratów wielkości K_x otrzymujemy dwie pary wartości x₀, yo, z których tylko jedna ma znaczenie fizykalne. Przez przesunięcie chwilowego punktu obrotu M do M' powiększa się oczekiwany promień krzywizny w punkcie podporowym J z rj na r'j , co

oznacza, że krzywizna K₃ = —~~ zmniejsza się na krzywiznę Kj =    ,

gdzie J = {A, B, C).

Stosunek rzeczywistej krzywizny toru do żądanej określa współczynnik jakości sterowania wyrażony zgodnie z rys. 5.41 jako lub (wyrażony w procentach)

R

w_tł = -~r- 100%