3582323324

1.    Cząstka o masie m znajduje się w jednowymiarowej symetrycznej studni potencjału o nieskończenie wysokich ściankach (-a/2<x<a/2) - porównaj podobne zadanie z zestawu 14. Znaleźć wartości własne energii i unormowane funkcje własne cząstki.

2.    Cząstka o masie m znajduje się w trójwymiarowej prostokątnej jamie potencjału o nieprzepuszczalnych ściankach (0<x<a, 0<y<b, 0<z<ć). Złożyć, że postać przestrzennej części funkcji falowej dana jest wzorem *F(x,y,z)=X(x) Y(y) Z(z). Znaleźć : a) wartości własne energii i unormowane funkcje własne cząstki, bjrozpatrzyć przypadek szczególny gdy a=b=c (obliczyć różnicę energii między trzecim a czwartym poziomem, liczbę stanów odpowiadających piątemu poziomowi, liczbę stanów w przedziale (E,E+dE).

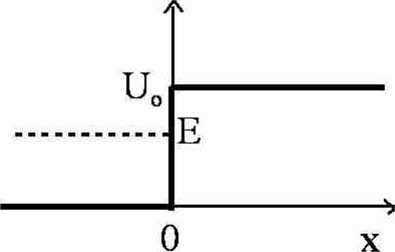
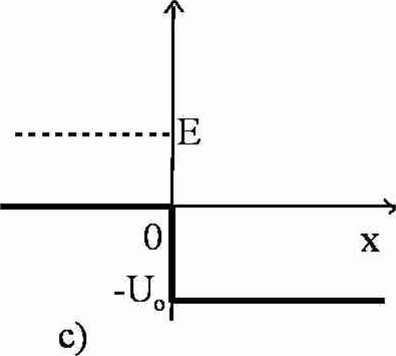
3.    Cząstka o masie m i energii E pada z lewej strony na próg potencjału o wysokości U„

(rys.2). Znaleźć: a) funkcje falowe dla: x<0 orazx>0, b) współczynnik transmisji T i współczynnik odbicia R w przypadku gdy E>U₀ oraz E<U_C, c) współczynnik transmisji T i współczynnik odbicia R dla U_o<0 (gdy E>0).

4.    Sprawdzić następujące reguły komutacyjne: a) [L_x, L_y] = i h L_{z 3} b*) [£.„, £²] = 0 ; gdzie:

Ł = - i h	(3 3 1 y— - z—	L = - i h	3 3 )	oraz Łz = - i h	3 3 1 x-— y—
X	3z 3yj	* y	3x 3z;		3y 3z

Znaleźć wartości własne operatora L₂

5.

.. 3

■ i h — wiedząc, że funkcja własna typu

3?

^um(ł)^{= ex}P(^cł) ₃ spełnia warunek periodyczności tzn. : u_m(^) = u_m(f + 2mit). Obliczyć ile wynosi stała c.

6. * Możliwe wartości rzutu momentu pędu na dowolną oś są równe mhgdzie: m= -l,

-1+1,    .,1-1,1. Biorąc pod uwagę, że rzutu są równoprawne i równie prawdopodobne,

wykazać, że w stanie z określoną wartością l średnia wartość średnia kwadratowa momentu pędu wynosi < L² > = h²1(1 + 1).

a-b)

rys.l