3582425848

		GEOMETRIA O	Twierdzenie Pitagorasa

Wtorek

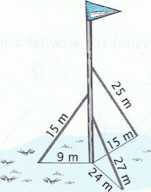
4. Wysoki maszt podtrzymują trzy liny przymocowane do niego na wysokościach lOm, 12 m i 20 m. Na rysunku podano długości lin. Maszt stoi pionowo. Ile lin nie jest napiętych?

□ A. jedna    □ C. trzy

□ B. dwie    □ D. wszystkie są napięte

5. Na rysunkach przedstawiono projekty trzech rodzajów płyt przeznaczonych na blaty stołów. Oceń, czy narysowane blaty mają kąty proste przy narożnikach.

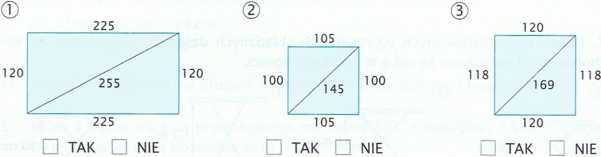
►► str. 181

6. Na którym z rysunków przedstawiony trójkąt me jest równoramienny?

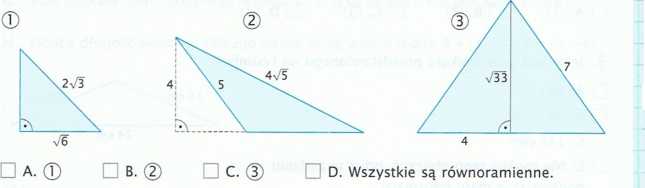
100