1636661162

6-2

Skompilował Janusz Mierczyński

6.2 Twierdzenia o istnieniu, jednoznaczności i

przedłużaniu rozwiązań dla układów równań różniczkowych zwyczajnych

Przez P będziemy (w tym podrozdziale) oznaczać prostopadłościan [zi,o — £1, #i,o + £i] x • • • x [x_njo — £_n, #n,o + £_n]j gdzie £i,..., e_n > 0.

Definicja. Funkcja wektorowa f: [to — S, to + ń] x P —> Rⁿ, gdzie S > 0, spełnia na [to — 5, to 4- <5] x P warunek Lipschitza względem x (jednostajnie po t), jeżeli istnieje L > 0 takie, że

||f(i,xi) - f(t,x₂)|| < L||xi -x₂||

dla wszystkich t G [to — <5, to + £] i wszystkich xi,X2 G P.

Fakt 6.1. Załóżmy, że pochodne cząstkowe dfi/dxj istnieją i są ciągle na [to — ó, to + <5] x P. Wówczas f spełnia na [to — ó,to ó] x P warunek Lipschitza względem x, ze stałą

L = nsup{ |J^-(t,x)| : i,j = 1,... ,n, t G [to — S, to -ł- 5], xgP}.

Twierdzenie 6.2 (Twierdzenie Picarda(-Lindelófa)). Niech f: [t₀ — 5, to + 6] x P —> Rⁿ będzie ciągłą funkcją wektorową spełniającą na [to — S,to + 6] x P warunek Lipschitza względem x ze stałą L jednostajnie po t. Wówczas istnieje dokładnie jedno rozwiązanie : [to — 77, to -t- 77] —> Rⁿ zagadnienia początkowego

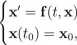
(URn-ZP)

gdzie rj = min{ń, jf-.

^    Ml    ' Mn '

Mi = sup{ |/j(t,x)| : t G [to — S,t₀ + <5],x G P}.

Dowód twierdzenia Picarda dla układów równań różniczkowych jest niemal wierną kopią dowodu tego twierdzenia dla równań (Tw. 3.2; należy tylko w odpowiednich miejscach zastąpić wartości bezwzględne normami).

Ciąg kolejnych przybliżeń to ciąg (</?_fc)£L₀ ciągłych funkcji wektorowych z [to — ?7, to + 77] w Rⁿ zdefiniowanych rekurencyjnie:

VoM = ^xo    Vi 6 [t₀ - i?, t₀ +1)]