2089

Twierdzenie (o zamianie całki podwójnej na całkę iterowaną) Z: /€C(/>). gdzie P = [a.£]x [c.d]

<*/b    ^

dy

P

oraz

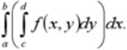
Uwaga

Każdą z całek występujących po prawej stronie powyższych wzorów nazywamy całką iterowaną.

Oznaczenia

1 Sybol da nazywamy elementem pola i oznaczamy dxdy.

2. Całki iterowane zapisujemy też w postaci.

*(•>    \ ozn^{d b}

J J /(*» y kv = J ch \/(.x, y )dx

e \.o    )    ca

dx

<d

J \f(x₉y)dy

jV/xJ/(.x,y>Ą

Przykład

0<.x<.2 0 £ y £ 3

Obliczyć całkę podwójną I = \\xy¹dxdy, gdzie P

Ponieważ f\x_yy)=xy^l e C(P), więc możemy zastosować twierdzenie o zamianie całki podwójnej na całkę iterowaną i wtedy

2    3    2 /, y 2

/ = JrfxJ.nV» =J| V | dx = f9xdx =

0    0    /o o

2

= 18 opracował Jacek Zańko