22892

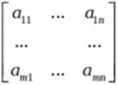
pochodna ma postać macierzy A(mxn): f'( x°) =

Z Twierdzenie o ciągłości funkcji różniczkowalnej.

Jeżeli funkcja f f : O. —> i ",(lc i ⁿ jest różniczkowalna w x°e i " to jest ona ciągła w tym punkcie, dowód:

Skoro f (x° + /i)-f(x°) =Ah+o(h) AUm^j^ = 0

To dla x€l/(x°| cftAx-x°=/i=>x = x° + /i zachodzi własność

||f(x)-f(x°)| = ( f(x°+/,)-f(x«))=||A>,|+||o(/,)|Sc|/.|+|o(/.)|=_C|x-x1|+|Hx-x»)||

||f(x)-f(x“)j<c||x-x»||₊|o(x-x°)|

x-> x° =>||x—X°|| —>0a||o( x — x°)|| ^0 =*■!/■( x) — f (x°|||->0=> f(x)-f[x°)-ciagla

1 Twierdzenie o pochodnej funkcji (podstawowe własności pochodnej).

Twierdzenie 1.:

Jeżeli funkcje f, g określone w pewnym otoczeniu punktu x° takie, że f,g:U[x° | —» i * i różniczkowalne w *° to ich suma i iloczyn przez skalar też są różniczkowalne, przy czym:

(f+fl)'(x°) = r(*°)+g'(*⁰)

(Af)-(x°)=Ar(x») dowód:

<kf _suny

( f + g)(x°+h)-(f₊g)(x°)    =    /■(x° + h) + g(x° + h)- f (x°) -g(x°) =

= [f(x° + h)-/‘(x⁰)]+[g(x⁰ + /i)-g(x⁰)]    = r(x^o)/i + o(h) + 0^,(x^o)h + o(/i) =

= f'(x⁰)h + g'(x⁰)h+o(h) =( f'[ x°) + $'( x⁰)) h + o( /i)

( /" + g] ( x° + /i) -( f + p)(x°) = ( /*'(x°) + g'(x°)| h + o( h) f + g-różniczkowalne

Twierdzenie Z (o pochodnej funkcji złożonej - reguła łańcucha):

i ".fic i    : A —» i ',Ac i ^m,(gOf){ x) = ^( f{ x)),x€ Q, <= A

Jeżeli f jest różniczkowalna w x° i g jest różniczkowalna w/=f(x°| to ( g Of) (x) jest

różniczkowalna w x°, gdzie [gOf)'(x) =5') f( x)| f'{x). dowód: