29350

Zi*Zj = (a*c) * (b*d) i. Zi-z₂ = (a-c) + (b-d) i, Z1Z2- (ac-bd) + (ad*bc) i.

Modułem liczby z = a + bi nazywamy liczbę

I Z | — -Ja'

Dzielenie Sczb zespolonych jest irodię trudniejsze. Laiwo można wykazać, że

\z\² -z ź

Oblczając iloraz — (zaMadając oczywiście, że Z₂ * 0) mnożymy licznik i mianownik lego ułamka przez spizężenie mianownika (liczby z₂).

Olrzymujemy wiedy następujący wzdr

2, (ac+bd)    (bc-ad)

Działania aiytmecyczne na Sczbach zespolonych są rozszerzeniem działali na liczbach rzeczywistych, tzn. w przypadku liczb rzeczywistych jest obojętne czy np. mnożymy je jako iczby rzeczywiste czy zespolone z częścią urojoną równą zero. Z podanych defiiicji działań na liczbach zespolonych wynika, że działania dodawania i mnożenia liczb zespolonych są łączne i przemienne oraz mnożenie jest rozdzielne względem dodawania. Zachowane są również znane własności odejmowania i dzielenia. Powyższe stwierdzenia powodują, że dla liczb zespolonych prawdziwe są wzory skróconego mnożenia, wzór dwumianowy Newtona, twierdzenie Bezout id.. Nie określamy natomiast nierówności liczb zespolonych innych niż rzeczywiste.

Przykład. 1.

Znajdź część rzeczywistą i urojoną liczby (5*2i)*(-3-i).

Aby znaleźć część rzeczywistą i urojoną należy dodać podane liczby zespolone. Otrzymujemy wówczas

(5*2i) * (-3-i) = (5-3) * (2-1) i = 2*i

Zatem część rzeczywista równa jest 2, a urojona 1.

Wykonaj działania (-1+7/) (4+10i).

Działania należy oczywiście wykonać w otyowiedniej kolejności (najpierw mnożenie, potem dodawanie i odejmowanie) pamiętając, że F=-l. (-l+7i)-(4+10i) = -1-4 + (-l)-lOi + 7i-4 + 7i-10i = •4 •lOi *281-70 = -74*18i

Przykład.3.

Jaka Sczba zespolona powstanie w wyniku podzielenia liczby 2i przez iczbę 1 +/'.

2/

W wyniku dzielenia otrzymujemy oczywiście ułamek -—₇ .

Wystarczy teraz pomnożyć Scznk i mianownik tego ułamka przez iczbę sprzężoną do liczby 1+i (z mianownika), czyi przez 1-i, a następnie uprościć otrzymane wyrażenie.

2/ _    2i(l-i) _ 2i -2i² _ 2i ->-2 _

1 + /    (l+i)(l-i) l-i² 2

Przy dzieleniu liczby 2 przez liczbę 1+/ otrzymujemy zatem liczbę l*i.

4. Postać trygonometryczna liczby zespolonej.

Zamiast określać liczbę zespoloną z = a*bi różną od zera poprzez podanie jej częśd rzeczywistej i urojonej możemy ją określić inaczej -współrzędnymi biegunowymi - podając odległość r punktu M(a, b) od początku układu współrzędnych oraz kąt p jaki tworzy wektor OM 1 dodatnim kiemnkiem osi Ox.

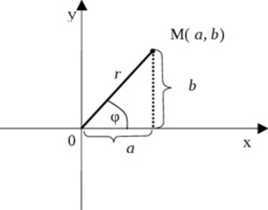
Wówczas zachodzązwiązki