105407

Wstęp teoretyczny.

Rozkład Poissona.

Rozkład Poissona jest rozkładem prawdopodobieństwa niezależnych zjawisk charakteryzujących się bardzo małym prawdopodobieństwem. Przykładem tego może być promieniowanie jonizujące, ponieważ źródło promieniowania zbudowane jest z pewnej ilości N atomów izotopu promieniotwórczego Rozpad pojedynczego jądra atomu próbki nie ma wpływu na rozpad jąder innych atomów.

W przypadku rozkładu Poissona rozkład zmiennej losowej X można przedstawić w postaci:

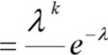
P.(X = k) ^v    k\

P.(X=k) = Ź/k! Exp(-X)

Dla rozpadu tego mamy, że :

E(X)=D²(X) = X

czyli wartość oczekiwana, wariacja i A. są równe.

Test Z-

Test x² jest testem ustalający stopień zgodności wyników otrzymanych na drodze empirycznej z wynikami uzyskanych z obliczeń teoretycznych. W przypadku rejestracji naszego doświadczenia ustalamy niezgodność rozkładu równomiernego.

Zmienna losowa ^'wynosi:

9

X²=£x„²

n*0

gdzie:

x„ = (k_n - k/10) / V(k/10)

k_n jest liczbą prób, w których otrzymano cyfrę n

wartość oczekiwana tego rozkładu E(X) = k/10, a dyspersja w przybliżeniu D(X) (1/k); czyli E(X) = 0. D(X) = 1.

Opis stanowiska pomiarowego.

Stanowisko przystosowane jest do badania prawidłowości statystycznych przy rejestracji promieniowania jonizującego. Zestaw składa się z następujących elementów:

•    licznika Geigera Mullera rejestrującego promieniowanie jonizujące,

•    izotopowego źródła promieniowania,

•    przelicznika połączonego z licznikiem G-M., któiy zlicza impulsy promieniowania,

•    mikrokomputera z programem realizującym trzy rozkłady statystyczne:

-    rozkład Poissona,

-    rozkład wykładniczy,