P1. Jaki materiał nazywamy izotropowym, a jaki anizotropowym?

Ciało izotropowe- ciało mające jednakową wytrzymałość na zmiany w każdym kierunku np. plastelina, powietrze, woda. Przeciwieństwem ciała izotropowego jest ciało a-izotropowe lub anizotropowe

2. Podać definicję sil biernych i czynnych.

Siły czynne - obciążenia,

Siły bierne - reakcje (zastępujące oddziaływanie sąsiednich, odrzuconych konstrukcji)

3. Podać definicję sił zewnętrznych i wewnętrznych.

Siły zewnętrzne (są to siły przyłożone do powierzchni rozpatrywanej bryły - siły powierzchniowe, oddziałujące przez styk lub też siły objętościowe, przyłożone w środkach ciężkości każdej cząstki objętości danej bryły i będące wynikiem działania pośredniego - grawitacja, bezwładność). Do sił zewnętrznych z punktu widzenia budowli zaliczamy zatem ciężar ludzi i urządzeń znajdujących się w danym pomieszczeniu, obciążenia śniegiem na połać dachową, obciążenia wiatrem ścian zewnętrznych. Do sił objętościowych zaliczamy głównie ciężar własny rozpatrywanej bryły (strop itp.) oraz siły bezwładności, jeśli dana bryła znajduje się w ruchu.

Siły wewnętrzne (są to siły występujące wewnątrz rozpatrywanej bryły - siły wzajemnego oddziaływania między jej cząstkami).

4. Co to jest odkształcenie, a co to jest przemieszczenie?

Odkształcenie- ZMIANA GEOMETRYCZNA

ogólnie: zmiana konfiguracji pierwotnej materiału; istnieje wiele miar odkształcenia; miarą wykorzystywaną w wytrzymałości materiałów jest tensor odkształceń Cauchy'ego: jest on linearyzacją tensorów odkształcenia Lagrange'a (we współrzędnych materialnych) i Eulera (we współrzędnych przestrzennych) przy utożsamieniu konfiguracji aktualnej z pierwotną (interpretacja jego składowych: patrz odkształcenie liniowe i kątowe)

przemieszczenie- ZMIANA POZYCJI BEZ ZMIANY GEOMETRYCZNEJ

(punktu) różnica między położeniem w konfiguracji końcowej i pierwotnej; obrazem jest wektor przemieszczenia

przemieszczenie możliwe

(punktu) wektor łączący dwa możliwe położenia punktu; zależy jedynie od więzów i nie musi być przemieszczeniem rzeczywistym punktu

przemieszczenie wirtualne

(przygotowane, pomyślane)(punktu) wektor współliniowy z prędkością wirtualną punktu (wynikającą z więzów układu)

5. Podać klasyfikację i definicję odkształceń.

odkształcenia plastyczne

odkształcenia trwałe; przeciwieństwo odkształceń sprężystych, znikających po zdjęciu obciążenia (po odciążeniu)

odkształcenie kątowe

(postaciowe) połowa zmiany kąta prostego, wyznaczonego kierunkami 2 osi układu współrzędnych

odkształcenie liniowe

wydłużenie (skrócenie) względne: względna zmiana długości odcinka o kierunku równoległym do osi układu współrzędnych

6. Podać definicję prostego rozciągania lub ściskania.

Rozciąganie (ściskanie) proste

przypadek w którym układ sił przekrojowych redukuje się do siły rozciągającej (ściskającej); stan naprężenia, odkształcenia i przemieszczenia przyjmujemy jak dla czystego rozciągania (ściskania) (na podstawie zasada de Saint-Venanta)

7. W jaki sposób można wyznaczyć naprężenia w przekroju poprzecznym pręta

rozciąganego lub ściskanego?

Naprężenia wyznaczamy po przez iloczyn działającej siły i pola powierzchni przekroju.

8. Podać prawo Hooke'a oraz odpowiadający mu opis analityczny.

Prawo Hooke'a - prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej nań siły jest wprost proporcjonalne do tej siły.

σ =  * E

9. Co to jest współczynnik sprężystości podłużnej i w jaki sposób można go wyznaczyć?

10. Jak można zdefiniować współczynnik Poisson'a ?

Bezwymiarowa stała materiałowa, określająca bezwzglądną wartość stosunku odkształceń poprzecznych do odkształcenia podłużnego.

11. W jakich granicach zawiera się współczynnik Poissona?

Od 0 do 0,5 dla realnych materiałów. Stal ok. 0,27.

12. Omówić zasadę de Saint-Vanauta.

Zjawisko równomiernego rozkadu napreń, niezalenie od sposobu

przyłożenia obciążenia, w dostatecznej odległości od miejsca przyłożenia sił. Używana przy rozciąganiu, ściskaniu.

13.Omówić zasadę superpozycji.

Całkowity skutek wynikający z działania wszystkich skutków jednocześnie jest równy sumie skutków wynikających z działania na układ z osobna.

14.Podać ogólny tok rozwiązywania układów statycznie niewyznaczalnych.

Do rozwizania zadania statycznie niewyznaczalnego trzeba odwołać się do metod dodatkowych, np.

prawa Hook'a, rozszerzalności termicznej (warunki fizyczne) czy nierozdzielności

przemieszczeń (warunek geometryczny).

15.Co nazywamy sztywnością na rozciąganie i ściskanie?

Jest to iloczyn modułu Younga i pola przekroju. Rozciąganie z +, ściskanie -.

16.Podać ogólne określenie kierunków głównych i naprężeń głównych.

Kierunki główne-

(własne) kierunki osi układu współrzędnych, w których macierz tensora jest macierzą diagonalną a współrzędne na przekątnej głównej są ekstremalne. Układ osi gównych to taki układ współrzędnych, który powstaje przez takie

przestrzenne zorientowanie osi aby w płaszczyznach prostopadłych do tych osi nie

występowały naprężenia ścinajce. Naprężeniami głównymi nazywamy naprężenia

normalne w tych płaszczyznach. Osie układu głównego oznaczamy 1, 2, 3, a

naprężenia w tych płaszczyznach

17.Zdefiniować stan naprężenia: jednoosiowy, dwuosiowy, przestrzenny.

Jednoosiowy-stan naprężenia w którym tylko jedno z naprężeń głównych jest niezerowe.

Dwuosiowy- wszystkie składowe stanu naprężenia leżą w jednej płaszczyźnie(np.x,y) , w kierunku z nie ma żadnych naprężeń.

Przestrzenny-określony za pomocą 9 składowych.

18.Podać wzory określające naprężenia normalne i styczne w przekroju ukośnym w jednoosiowym stanie naprężenia.

19.Jaka jest zależność między naprężeniami normapnymi i stycznymi?

Wektor naprężenia normalnego działa prostopadle do podstawy a wektor styczny równolegle.

24. Czym charakteryzuje się stan czystego ścinania?

Jest to stan w którym występują tylko naprężenia scinające. Zawsze doprowadza do zmiany postaci, może doprowadzać do odkształceń trwałych.

26. Co to jest współczynnik sprężystości poprzecznej, jak można go wyznaczyć i od

jakich stałych materiałowych zależy?

Współczynnik sprężystości poprzecznej to moduł Kirchoffa - współczynnik uzależniający odkształcenia podstawowe materiału od naprężenia, jakie w nim występuje.

T- naprężenie styczne

γ odkształcenie postaciowe

v-wskaznik Poisona

E-moduł Youbga

36. Podać wzór wydłużenie walcowej sprężyny śrubowej.

S=k(x+δ) k - współczynnik proporcjonalności między siłą przyciągającą a wychyleniem spręzyny x - wychylenie z położenia równowagi δ - wydłużenie statyczne sprężyny

37. Podać definicję zginania prostego i czystego.

Zginanie czyste obciążenie pręta pryzmatycznego obciążeniem powierzchniowym przyłożonym do denek pręta, liniowo zmiennym (po wysokości przekroju), redukującym się do momentu zginającego, równoległego do głównej centralnej osi bezwładności; zagadnienie brzegowe teorii sprężystości daje się rozwiązać ściśle (stąd nazwa: czyste)

Zginanie proste układ sił przekrojowych redukuje się do momentu zginającego, działającego równolegle do głównej centralnej osi bezwładności; na podstawie zasady de Saint-Venanta przyjmuje się rozwiązanie jak dla zginania czystego.

38. Podać definicję momentu zginającego i siły poprzecznej w przekroju belki zginanej.

moment zginający (gnący), moment, którego wektor działa w płaszczyźnie przekroju poprzecznego

siła poprzeczna (tnąca, ścinająca) składowa siły przekrojowej na jedną z osi głównych centralnych bezwładności przekroju; rzut wypadkowej wszystkich sił, działających na odrzuconą część układu, na kierunek jednej z głównych centralnych osi bezwładności przekroju; znak ustalany na podstawie przyjętej konwencji znakowania sił przekrojowych; zerowanie się siły poprzecznej oznacza ekstremum momentu zginającego

39. Jak określa się moment zginający i siłę poprzeczną w danym przekroju belki?

Określa się je mianem wtórnych sił przekrojowych

40. Podać definicję czystego zginania oraz założenia przyjmowane przy wyprowadzaniu

wzorów określających naprężenia normalne w przekroju poprzecznym belki zginanej.

Zginanie czyste obciążenie pręta pryzmatycznego obciążeniem powierzchniowym przyłożonym do denek pręta, liniowo zmiennym (po wysokości przekroju), redukującym się do momentu zginającego, równoległego do głównej centralnej osi bezwładności; zagadnienie brzegowe teorii sprężystości daje się rozwiązać ściśle (stąd nazwa: czyste)

Założenia: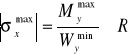

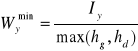
gdzie W_y - wskaźnik wytrzymałości przekroju, R - wytrzymałość materiału na rozciąganie.

41. Co to jest warstwa obojętna?

Jest to warstwa prostopadła do płaszczyzny działania momentu zginającego, w której włókna

nie ulegają odkształceniom  naprężenia = 0

42. Co to jest oś obojętna?

Oś obojętna jest to miejsce przecięcia płaszczyzny naprężeń z płaszczyzną przekroju poprzecznego, czyli miejsce geometryczne punktów, w których naprężenia są równe zeru. 

43. W jaki sposób określa się położenie osi obojętnej?

Oś obojętna pokrywa się z kierunkiem działania wektora momentu tylko w przekrojach, dla których I_y =  I_z. Jeżeli I_y > I_z, oś obojętna odchyla się w kierunku osi z, natomiast dla przekrojów w których I_y < I_z, odchylenie następuje w kierunku osi y. Na rys.4 pokazano różne położenia osi obojętnej w zależności od wartości głównych centralnych momentów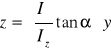
bezwładności. Można ją wyznaczyć ze wzoru:

35. Wyprowadzić wzór na wskaźnik wytrzymałości na skręcanie?

biegunowy moment bezwładności dla pełnego elementu:
, dla drążonego elementu:

44. Podać wzór opisujący krzywiznę belki w przypadku czystego zginania.

45. Na podstawie jakiego wzoru określa się wartość naprężenia normalnego w przekroju belki zginanej i w którym miejscu przekroju osiągają one wartość największą?

Największe naprężenia wystąpią w miejscu przekroju najbardziej odległym od osi obojętnej.

46. Co to jest wskaźnik wytrzymałości na zginanie?

Wskaźnik wytrzymałości na zginanie- stosunek momentu bezwładności przekroju wzglęgem osi obojętnej do osi odległości włókien skrajnych od tej belki.

Wx

47.Co to jest sztywność na zginanie?

E*J = moment bezwładności* moduł Younga

52.Co nazywamy lini ugięcia belki?

Linina ugięcia belki- odkształcona oś. W czsie pracy belka ulega odkształceniu. Pocztąktowko prostoliniowa oś belki zmienia się na krzywoliniową. Krzywa nazywa się linią ugięcia osi belki. Przemieszczeniem środka ciężkości przekroju w kierunku prostopadłym do osi belki nazywamy ugięciem belki a największe ugięcie strzałką ugięcia belki.

53.Podać założenia przy wprowadzaniu przybliżonego równania różniczkowego lini ugięcia.

Ugięcia są bardzo małe w porównaniu z długością belki, wobec czego są małe kąty nagięcia

V=tgV= W`

54.Co to jest kąt obrotu?

Kąt ,o jaki obrócą się względem siebie końcowe przekroje poprzeczne pręta.

55. Jakie musz być spełnione warunki przy zastosowaniu metody Clebscha?

1. Zaczynamy od jednego krańca belki i po kolejki wypisujemy wszystko co działa na tę belkę w postaci:
O(x-a)°
O - siła.
a - odległość siły od krańca belki
o - potęga zależna od rodzaju siły.
o dla momentów wynosi 0, dla sił 1 dla obciążeń ciągłych 2(dodatkowo wartość obciążenia ciągłego należy podzielić przez dwa).

Rodzaj	Wartość (O)	Potęga (o)	Zapis w metodzie Clebscha
Moment	M	0	M(x − a)0
Siła	P	1	P(x − a)1
Obciążenie ciągłe	q	2

2. Przy całkowaniu nie rozwijamy wyrazów w nawiasach odpowiedzialnych za położenie.

56. Jak wyznacza się ugięcie belki w przypadku zginania ukośnego?

Kożystając z zasady superpozycji. Np. W belce w której główne, centralne osie y i z są znane i rozdzielają obciążenia Q1, Q2 na działające w płaszczyźnie x,z tj. P1, P2 i yz tj. H1, H2 mamy każdym z dwóch przypadków do czynienia ze zgięciem prostym w odpowiedniej płaszczyźnie.

Wypadkowe ugięcie fx w przekroju określonym odciętą x jest równe goemetrycznej sumie ugięć w(x) i v(x).Linie ugięcia belki jest na ogół krzywą przestrzenna i staje się płaską tylko wtedy, gdy stosunek ugięć v(x)/w(x) jest niezależny od x

57.Co to jest wytężenie ?

Ogół zmian fizycznych i strukturalnych jakie nastąpiły w materiale w trakcie jego wymuszonej deformacji.

58.

59.Co nazywamy naprężeniem zredukowanym?

Naprężenie zredukowane- fikcyjne naprężenie(zastępcze).

73. Co to są układy liniowo-sprężyste?

Układ, który po zdjęciu obciążenia powraca do konfiguracji pierwotnej.

64.Co to jest wyboczenie?

Przemieszczenia układu powstałe w wyniku utraty stateczności.

65. Co to jest siła krytyczna?

siła przy której pręt (konstrukcja) traci stateczność

66. Podać i omówić przykłady wyboczenia.

A-pręt zamocowany na obu końcach przegubowo lr= l

B-pręt z jednym końcem utwuerdzonym, drugim zamocowanym przegubowo lr=0,7l

C-pręt na obu koncach utwierdzony lr=0,5l

D-pręt utwierdzony jednym końcem lr=2l

67. Podac i omówić wzór Eulera.

E- moduł Younga

lr- długośc zredukowana pręta, zależna od sposobu jego zamocowania

Jmin-najmniejszy, głowny moment bezwładności przekroju pręta

68.Zdefiniować smukłość pręta.

Smukłość T jest liczbą charakteryzującą pręt. Zależy ona od właściwości przekroju, długości wyboczeniowej pręta.

T= lr/i min

lr-długość zredukowana

i min- minimalny promień bezwładności przekroju poprzecznego pręta.

69, Co to jest smukłość graniczna?

stała materiałowa, bezwymiarowa, określająca granicę między liniowo sprężystym i sprężysto-plastycznym zakresem pracy pręta ściskanego; wartość dla stali ok.110 .

Dla większości materiałów, smukłością graniczna dla wyboczenia niesprężystego jest gdzie:

E - współczynnik sprężystości wzdłużnej

Rn - maksymalne naprężenie, dla którego można przyjąć ważność prawa Hooke'a.

71.Kiedy występuje wyboczenie niesprężyste?

Wyboczenie niesprężyste występuje dla smukłości   gr .

Wyboczenie niesprężyste występuje dla smukłości   gr .

49.Narysować rozkład naprężeń stycznych przy zginaniu belki o przekroju prostokątnym

i teowym.

60.Wymienić i omówić najczęściej stosowane hipotezy wytężeniowe.

hipoteza wytężeniowa Hubera

miarą wytężenia jest gęstość energii odkształcenia postaciowego; stan niebezpieczny obrazowany jest: w przestrzeni Haigha-Beckera pobocznicą walca nieskończonej długości o przekroju kołowym i osi równo nachylonej do osi układu, na płaszczyźnie dewiatorowej kołem, w p.s.n. elipsą; odpowiednia dla materiałów plastycznych

60.Wymienić i omówić najczęściej stosowane hipotezy wytężeniowe.

hipoteza wytężeniowa Hubera

miarą wytężenia jest gęstość energii odkształcenia postaciowego; stan niebezpieczny obrazowany jest: w przestrzeni Haigha-Beckera pobocznicą walca nieskończonej długości o przekroju kołowym i osi równo nachylonej do osi układu, na płaszczyźnie dewiatorowej kołem, w p.s.n. elipsą; odpowiednia dla materiałów plastycznych

hipoteza wytężeniowa Mohra-Coulomba

miarą wytężenia jest wektor naprężenia: jego składowa normalna i styczna; stan niebezpieczny wg Mohra obrazowany jest w układzie |τ|(σ) krzywoliniową obwiednią (wewnątrz której zawierają się wszystkie koła Mohra dla stanów zwanych z tego powodu stanami dopuszczalnymi); hipoteza jest odpowiednia dla materiałów kruchych; liniowa aproksymacja obwiedni (stanów niebezpiecznych) w układzie |τ|(σ) stanowi podstawę hipotezy Coulomba, stosowanej dla gruntu

---