4672948908

Twierdzenie sinusów i cosinusów

Teraz porównujemy obydwa (tzn. (*), (*')) wzory na pole tego samego trójkąta i wyliczamy a.

Ml2^ia+20)/:2^

272(19 + 872)⁽" * ^{20) =}

fony    ma po!c zawsze Ufo samo nc/a!cto+

od togo. jakim wzorom fo poslugujomy. Dlatego moina O IO pozdwnaC

Wyliczamy a.

fl + 20

12

19 + 872 n + 20 = 12(19 + 875 ) n + 20 = 228 + 96 72

« + 20 = 228 + 96 75 /-20 </ = 228 + 96 75 -20 Czyli« = 208 + 96 75 Ad 3®

$=£*£ l-ĄR 4R

S • 4 R = obc /AS

Stosujemy wzót na polo trdjfou. znaleziony w-popfzednim zadaniu. Wyłgamy z togo wzocu fL Podstauńamy do wwu dano.

(208 + 9675 ) ’$■ \t

*,-2^72

(208 + 96 72 ) -2    208 + 9675

”    572    72

(208 + 9675) 75 208 -72 +96 -2 ^--7TT2 ⁼    2

₌ JUM^_jLW _{= |04x5 + 96}

5

Ad 4°

~~ = 2R /-sin p

Sin |>    Korzystamy z tw. sinusdw.

Stąd wyliczamy sin |i b = 2R sin p 1:2R

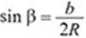
Czyli

sin y

sin p = ---=-£

Ż(104V +96) 104 V2

= 2/? / siny

Do wrotu podstawiamy dane. _ 1

+ 96 26>/2 +24

Stąd wyliczamy sin y c = 2R sin y /:2/?

c    T2*    _    6__3_

^{1 /}    2R 7(104    +96) 104/2 + 96 52^+48

Odpowiedź

«c = 208♦96 J5. sin p -    ^{sin 7 =} ś^TT

$= 24yfl ,R= 104>/2 +96

TWIERDZENIE COSINUSÓW

c

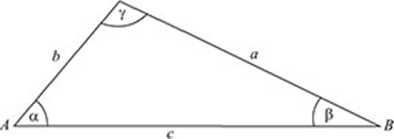
W dowolnym trójkącie między bokami i kątami zachodzą związki: a^} = b^} + c² — 2/ktcos a b* = a* + c¹ - 2r/ccos (i c* = a* + b* - lab cos y

(kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn tych boków i cosi-nusa kąta zawartego między nimi).

157