5020058113

Trójkąty sferyczne

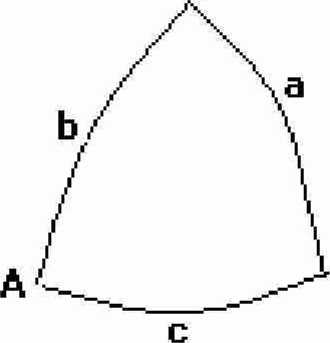
B

I. BBB (3 x twierdzenie cosinusów dla boków)

cosa = cosicosct sini ■ sine • cos A sini-sine • cos = cos a- cosi-cosc cos a- cosi-cosc

COS^ ;

sini • sine

II. KKK (3 x twierdzenie cosinusów dla kątów)

cos^4= -cosS-cosCt sini? • sinC- cosa sini? • sinC-cosa = cosyił cosU-cosC cosylł cosi? - cosC

cos a:

sinB - sinC

III. KBK (AbC)

1.    cosi?= - cosy4-cosC + sinyi-sinC -cosi

2.    AbCa - tw. Cotangensów

cosi • cosC = sini • ctga- sinC• ctgA sini • ctga = cosi • cosC + sinC • ctgA cosi -cosC t smCctgA

ctga

tga

sini

sini

cosi• cosCł sinC• ctgA

3. cAbC

cos^■ cosi = sini • ctgc- sinyi• ctgC sini• ctgc = cos.4• cosi ł sin.<4• ctgC cos^4 ■ cosi + siny4 • ctgC

ctgc

tgc

sini

sini

cos./4 • cosi ł sin.4 • ctgC