4292417160

6 Całki krzywoliniowe

Całka krzywoliniowa nieskierowana

Jeśli krzywa na płaszczyźnie ma parametryzację (x(t),y(t)), gdzie t e [a,6] i x(t), y(t) są różniczko-walne podanym przedziale, to nazwiemy ją lukiem gładkim. Jeśli krzywa składa się z łuków gładkich, to nazywamy ją krzywą regularną. Ponadto, jeśli za początek krzywej przyjmiemy punkt (x(a),y(a)), to mówimy, że krzywa jest zorientowana dodatnio.

Niech L będzie krzywą regularną. Wówczas całką krzywoliniową nieskierowaną z funkcji f(x,y) nazwiemy wyrażenie:

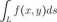
Interpretacja fizyczna to masa krzywej L o gęstości f(x,y), a interpretacja geometryczna to pole powierzchni znajdującej się między krzywą L. a fragmentem powierzchni z = f(x, y) znajdującym się nad krzywą L.

Praktyczny sposób liczenia takich całek jest bardzo prosty i sprowadza się do podstawienia do wzoru. Jeśli mamy parametryzację luku (x(t),2/(<)), gdzie t e [a,6], to:

f_LHx,y)ds = jf ‘

W szczególności zaś jeśli luk da się zadać równaniem y = g(x), gdzie a < x < b, to powyższy wzór wygląda tak:

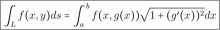
Przykład:

Policzmy masę okręgu x² + y² = 4 o gęstości /(x, y) = _xi *₂₊₁. Oczywiście parametryzacja to x(t) = 2cost,y(t) = 2sint, gdzie t € [0,27r). Mamy: f(x(t),y(t)) = g oraz x'{t) = -2sint i y'{t) = 2cost, a zatem \J{x'{t))² + {y'{t))² = 2>/2. Tak więc poprzedni wzór daje nam: h H*. y)ds = /₀²’ i' 2s/2dt =

12