9414912692

18

WYKŁAD 1. CIĄGI I SZEREGI LICZBOWE

Rozwiązanie. Stosujemy kryterium Cauchy’ego

lim \/a_n — lim

n—► oo    n-*oo

lim

n—>oo

lim

71—>00

szereg jest zatem zbieżny.

□

Przykład 1.21. Zbadamy zbieżność szeregu

e

2ⁿ3ⁿ⁺¹

5ⁿ⁺²

Rozwiązanie. Stosujemy kryterium Cauchy’ego

lim y/a_n = lim

n—>oo    n—> oo

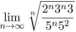
2 • 3 \/3 5 \/5²

6

5

> 1

□

szereg jest zatem rozbieżny.

Szeregi naprzemienne

Szeregiem naprzemiennym nazywamy szereg postaci

y^(-l)ⁿ⁺1q_n = ai - 02 + a3 - a₄ + ■ ■ ■

n= 1

gdzie a_n > O dla każdego n € N. Zbieżność szeregów naprzemiennych rozstrzyga następujące

Kryterium Leibniza

Rozpatrzmy szereg naprzemienny

E(-l)"⁺¹a~

71=1

Jeżeli ciąg {a_n} jest malejący oraz lim a_n = O to szereg jest zbieżny.

71—>00

Przykład 1.22. Zbadać zbieżność szeregu

1

n'

E(-D"⁺¹

71=1

Rozwiązanie. Ciąg a_n = ^ jest malejący oraz lim 1/n — 0. Stąd oraz z kryterium Leibniza

ⁿ    n—>oo

wynika, że szereg jest zbieżny.    □