1108720256

- różnice w wartościach tych samych metryk otrzymanych z porównania badania przedzabiegowego z wczesnym badaniem kontrolnym i końcowym po zabiegu powinny maleć w przypadku poprawy stanu zdrowia pacjenta ocenionej subiektywnie przez lekarzy.

Celem całości analizy sygnałów akustycznych mowy prawidłowej jak i patologicznej, w niniejszej pracy jest obiektywne stwierdzenie (oparte o przedstawione metryki), czy sygnał mowy u pacjentów poddanych operacji:

1)    polepszył się, tzn. odległość wg wybranej metryki sygnału zdeformowanego od wzorca sygnału mowy przed operacją jest większa niż podczas wczesnego i końcowego badania dokonanego po zabiegu przy jednoczesnym subiektywnym stwierdzeniu poprawy mowy pacjenta,

2)    pogorszył się, tzn. odległość wg wybranej metryki odległości sygnału zdeformowanego od wzorca sygnału mowy przed operacją jest mniejsza niż podczas wczesnego i końcowego badania dokonanego po zabiegu przy jednoczesnym subiektywnym stwierdzeniu pogorszenia mowy pacjenta.

Przyjmuje się, że im większa wartość odległości wg wybranej metryki sygnału zdeformowanego od sygnału wzorca, tym większa miara niepodobieństwa tych sygnałów. W przypadku wartości odległości bliskiej zeru, między badanymi sygnałami, należy zinterpretować ich podobieństwo jako tożsame.

2.3. Odwzorowanie Sammona - wizualizacja wielozmiennych danych na płaszczyźnie.

Odwzorowanie Sammona [96] umożliwia przedstawienie danych wielozmiennych (N - wymiarowych) na płaszczyźnie (układzie R²). Z uwagi na fakt, że struktury wielowymiarowe nie poddają się ludzkiej interpretacji, zawodzi zdolność człowieka do wyobrażenia sobie położenia tych danych (punktów) w przestrzeni N - wymiarowej. Istnieje zatem problem zrozumiałego i przystępnego graficznego zobrazowania tego typu danych. Zakładając, że dany jest zbiór n wektorów N - wymiarowych x_t = (x_n,...,x_jN)^T dla / = 1,2,3,...,w, to odpowiednio do nich definiuje się n wektorów w przestrzeni dwuwymiarowej, oznaczając przez y_t = (y_n,y_l2y dla / = 1,2,3,...,n. Odległości pomiędzy poszczególnymi wektorami w przestrzeni N - wymiarowej oznaczono jak d* =d(x,,Xj), a w przestrzeni dwuwymiarowej jako dj =d(y_l,y_J). Do określenia odległości między wektorami stosuje się metrykę Euklidesa (2.6). Odwzorowanie polega na takim doborze wektorów y, aby zminimalizować funkcję błędu E zdefiniowaną w postaci:

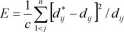
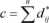
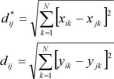
(2.12)

gdzie:

(2.13)

(2.14)

(2.15) w których x,*- k-ta składowa wektora Xj, yk-ta składowa wektora yi

16